
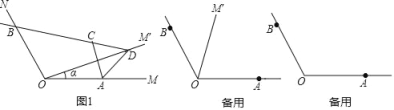
【题目】如图,已知∠MON=120°,点A,B分別在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°,且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD.
(1)求证:AD=CD;
(2)如图1,当0°<α<60°时,试证明∠ACD的大小是一个定值;
(3)当60°<α<120°时,(2)中的结论还成立吗?请补全图形并说明理由;
(4)△ACD面积的最大值为 .(直接写出结果)
【答案】(1)详见解析;(2)详见解析;(3)结论不变;(4)![]() a2.
a2.
【解析】
(1)证明△ODC≌△ODA(SSS)即可解决问题;
(2)如图1中,由题意OB=OA=OC,以O为圆心OC为半径作⊙O,在⊙O上OA的下方取一点H,连接HB,HA.理由圆周角定理,圆内接四边形的性质即可解决问题;
(3)结论不变.如图2中,由题意OB=OA=OC,以O为圆心OC为半径作⊙O,理由圆周角定理即可解决问题;
(4)证明△ACD是等边三角形,可知当AC为⊙O的直径时,△ACD的面积最大.
(1)如图1中,连接OC,

∵点A与点C关于直线OD对称,
∴OC=OA,DC=DA,
∵OD=OD,
∴△ODC≌△ODA(SSS),
∴DC=DA;
(2)如图1中,由题意OB=OA=OC,以O为圆心OC为半径作⊙O,在⊙O上OA的下方取一点H,连接HB,HA.
∵∠H=![]() ∠AOB=60°,∠H+∠BCA=180°,
∠AOB=60°,∠H+∠BCA=180°,
∴∠BCH=120°,
∴∠ACD=60°,
∴∠ACD是定值;
(3)结论不变.
理由:如图2中,由题意OB=OA=OC,以O为圆心OC为半径作⊙O,

∵∠AOB=120°,∠ACB=![]() ∠AOB,
∠AOB,
∴∠ACB=60°,
故结论成立;
(4)由(1)(2)可知:DC=DA,∠ACD=60°,
∴△ACD是等边三角形,
∴当AC为⊙O的直径时,△ACD的面积最大,
∴S△ADC=![]() ×(2a)2=
×(2a)2=![]() a2.
a2.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°方向上,那么该车继续行驶( )分钟可使汽车到达离楼H距离最近的位置.
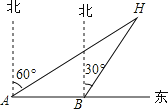
A.60 B.30 C.15 D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CP∥AB,在CP上截取CF=CD,连接BF.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,BC=![]() ,求线段CD和BF的长.
,求线段CD和BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
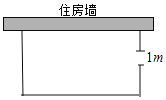
【题目】如图,一农户要建一个矩形鸭舍,鸭舍的一边利用长为13m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门![]() 所围矩形鸭舍的长、宽分别为多少时,鸭舍面积为
所围矩形鸭舍的长、宽分别为多少时,鸭舍面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
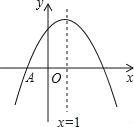
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
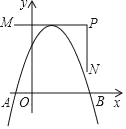
【题目】如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
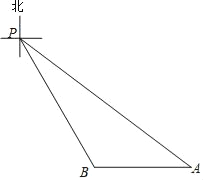
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.

(1)请写出这个反比例函数的解析式;
(2)蓄电池的电压是多少?
(3)完成下表:

(4)如果以此蓄电池为电源的用电器的限制电流不能超过10 A,那么用电器可变电阻应控制在什么范围?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com