
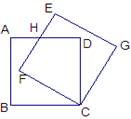
如下图,边长为3的正方形ABCD绕点C按顺时针方向旋转30º后得到正方形EFCG,EF交AD于点H,那么DH的长为 。
【解析】
试题分析:连接CH,由旋转的性质可知∠BCF=30°,则∠DCF=60°,利用“HL”证明Rt△CDH≌Rt△CFH,可知∠DCH=∠FCH=30°,解Rt△CDH即可得到结果.
如图,连接CH,
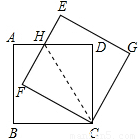
∵正方形ABCD绕点C按顺时针方向旋转30°,
∴∠BCF=30°,则∠DCF=60°,
在Rt△CDH和Rt△CFH中,
CD=CF,CH=CH,
∴Rt△CDH≌Rt△CFH,
∴∠DCH=∠FCH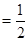 ∠DCF=30°,
∠DCF=30°,
∴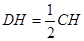 ,
,
设 ,则
,则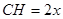
在Rt△CDH中,
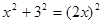 ,
,
解得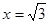 ,
,
则DH的长为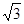
考点:本题考查了旋转的性质,正方形的性质,含30°角的直角三角形的性质,勾股定理
点评:解答本题的关键是熟练掌握含30°角的直角三角形的性质:30°角的所对的直角边等于斜边的一半。


科目:初中数学 来源: 题型:
| 5 |
| 5 |

| 5 |
| 5 |
| 5 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:江苏省常州市部分学校2011届中考模拟联考数学试题 题型:044
如图,把一个边长为2![]() 的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).

(1)求抛物线c1的解析式及点M、N的坐标;
(2)如下图,另一个边长为2![]() 的正方形
的正方形![]() 的中心G在点M上,
的中心G在点M上,![]() 、
、![]() 在x轴的负半轴上(
在x轴的负半轴上(![]() 在
在![]() 的左边),点
的左边),点![]() 在第三象限,当点G沿着抛物线c1从点M移到点N,正方形
在第三象限,当点G沿着抛物线c1从点M移到点N,正方形![]() 随之移动,移动中
随之移动,移动中![]()
![]() 始终与x轴平行.
始终与x轴平行.
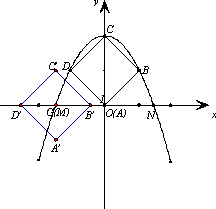
①直接写出点C’、D’移动路线形成的抛物线C(C’)、C(D’)的函数关系式;
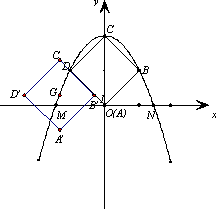
②如图,当正方形![]() 第一次移动到与正方形ABCD有一边在同一直线上时,求点G的坐标.
第一次移动到与正方形ABCD有一边在同一直线上时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
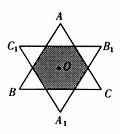
如下图,O是边长为1的正△ABC的中心,将△ABC绕点O逆时针方向旋转180°,得△A1B1C1,则△A1B1C1与△ABC重叠部分(图中阴影部分)的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com