
分析 设旅游团的人数是x人,旅行社可以获得营业额为W元,根据条件:30人起组团,可知x≥30,分两种情况:①当x=30时,没有优惠,单价为800元,总营业额为W=30×800=24000,②当x>30时,根据每人单价不能低于600元,列式为800-10(x-30)≥600,得x≤50,此时人数的取值为:30<x≤50,先表示W与x的关系式,并根据取值计算最值.
解答 解:设旅游团的人数是x人,旅行社可以获得营业额为W元,
由题意可知:x≥30,
①当x=30时,W=30×800=24000,
②当x>30时,
根据题意得:800-10(x-30)≥600,
x≤50,
此时30<x≤50,
W=x[800-10(x-30)]=-10x2+1100x=-10(x2-110x+552-552)=-10(x-55)2+30250,
∵-10<0,
∴当x<55时,W随x增大而增大,
∴当x=50时,W有最大值,
W最大值=-10(50-55)2+30250=30000,
24000<30000,
综上所述,当一个旅游团的人数是50时,旅行社可以获得最大营业额.
点评 本题是二次函数的应用,属于利润问题,解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围,如本题通过计算取值为:30<x≤50,小于顶点坐标的横坐标,因此根据增减性进行判断.


科目:初中数学 来源: 题型:解答题
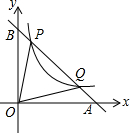 如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于P、Q(4,m)两点,与两坐标轴交于A、B两点,点(0.5,8)在双曲线上.
如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于P、Q(4,m)两点,与两坐标轴交于A、B两点,点(0.5,8)在双曲线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
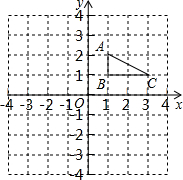 △ABC在平面直角坐标系中的位置如图所示,其中A(1,2),B(1,1),C(3,1),画出△ABC绕原点O顺时针旋转90°后得到△A′B′C′.
△ABC在平面直角坐标系中的位置如图所示,其中A(1,2),B(1,1),C(3,1),画出△ABC绕原点O顺时针旋转90°后得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 消费金额(元) | 300-400 | 400-500 | 500-600 | 600-700 | … | … |
| 返还金额(元) | 30 | 60 | 100 | 130 | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=30°,AB=p,BC=q,且p、q是关于x的方程x2-mx+3m=0的两个实数根,若|p+2q|=$\frac{1}{3}$pq+6,试在△ABC内找一点P,使P到A、B、C三点的距离之和最小,求出最小值并说明理由.
如图,在△ABC中,∠ABC=30°,AB=p,BC=q,且p、q是关于x的方程x2-mx+3m=0的两个实数根,若|p+2q|=$\frac{1}{3}$pq+6,试在△ABC内找一点P,使P到A、B、C三点的距离之和最小,求出最小值并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com