
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

【答案】(1)解析式为y=﹣x2+6x﹣5,对称轴:直线x=3,顶点坐标(3,4);(2)k=![]() 或k=
或k=![]() ;(3)当x=2时,SPMN最大,最大值为8,此时P(2,3);(4)①当x≤1或3≤x≤5时y随x的增大而增大;②当
;(3)当x=2时,SPMN最大,最大值为8,此时P(2,3);(4)①当x≤1或3≤x≤5时y随x的增大而增大;②当![]() <k<1时,直线l与图象L2有四个交点.
<k<1时,直线l与图象L2有四个交点.
【解析】
(1)根据待定系数法,可得函数解析式;(2)根据线段的比,可得直线与x轴的交点,根据自变量与函数值的对应关系,可得答案;(3)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PH,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案;(4)①根据函数图象的增减趋势,可得答案;②根据函数图象的交点,可得直线经过D,B点,根据自变量与函数值的对应关系,可得相应的k值,可得答案.
(1)∵抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)
∴y=﹣(x﹣1)(x﹣5)=﹣(x﹣3)2+4,
∴抛物线L1的解析式为y=﹣x2+6x﹣5
对称轴:直线x=3
顶点坐标(3,4);
(2)∵直线l将线段AB分成1:3两部分,则l经过点(2,0)或(4,0),
∴0=2k﹣5或0=4 k﹣5
∴k=![]() 或k=
或k=![]() .
.
(3)如图1
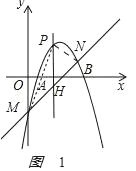 ,
,
设P(x,﹣x2+6x﹣5)是抛物线位于直线上方的一点,
解方程组![]() ,解得
,解得
![]() 或
或![]()
不妨设M(0,﹣5)、N(4,3)
∴0<x<4
过P做PH⊥x轴交直线l于点H,
则H(x,2x﹣5),
PH=﹣x2+6x﹣5﹣(2x﹣5)=﹣x2+4x,
S△PMN=![]() PHxN
PHxN
=![]() (﹣x2+4x)×4
(﹣x2+4x)×4
=﹣2(x﹣2)2+8
∵0<x<4
∴当x=2时,SPMN最大,最大值为8,此时P(2,3)
(4)如图2
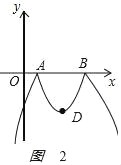 ,
,
A(1,0),B(5,0).由翻折,得D(3,﹣4),
①当x≤1或3≤x≤5时y随x的增大而增大
②当y=kx﹣5过D点时,3k﹣5=﹣4,解得k=![]() ,
,
当y=kx﹣5过B点时,5k﹣5=0,解得k=1,
直线与抛物线的交点在BD之间时有四个交点,即![]() <k<1,
<k<1,
当![]() <k<1时,直线l与图象L2有四个交点.
<k<1时,直线l与图象L2有四个交点.


科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
D为AB边上一点.
(1)求证:△ACE≌△BCD
(2)若AD=6,BD=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(1)、九(2)两班的班长交流了为四川安雅地震灾区捐款的情况:
(Ⅰ)九(1)班班长说:“我们班捐款总数为1200元,我们班人数比你们班多8人.”
(Ⅱ)九(2)班班长说:“我们班捐款总数也为1200元,我们班人均捐款比你们班人均捐款多20%.”
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=2x+1与坐标轴交于A,C两点,直线l2: y2=-x-2与坐标轴交于B,D两点,两直线交于P点.

(1)求P点的坐标;
(2)求△APB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线1垂直于x轴,垂足为M(m,0),点A(﹣1.0)关于直线的对称点为A′.
探究:(1)当m=0时,A′的坐标为 ;
(2)当m=1时,A′的坐标为 ;
(3)当m=2时,A′的坐标为 ;
发现:对于任意的m,A′的坐标为 .
解决问题:若A(﹣1,0)B(﹣5,0),C(6,0),D(15,0),将线段AB沿直线l翻折得到线段A′B′,若线段A′B′与线段CD重合部分的长为2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是⊙O上一点,直线AE经过点D,直线AB经过圆心O,交⊙O于B,C两点,CE⊥AE,垂足为点E,交⊙O于点F,∠BCD=∠DCF
(1)求∠A+∠BOD的度数;
(2)若sin∠DCE=![]() ,⊙O的半径为5,求线段AB的长.
,⊙O的半径为5,求线段AB的长.
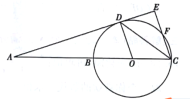
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3经过点A,B,C,已知A(-1,0),B(3,0).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,在(2)的条件下,延长DP交x轴于点F,M(m,0)是x轴上一动点,N 是线段DF上一点,当△BDC的面积最大时,若∠MNC=90°,请直接写出实数m的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com