
【题目】抛物线y=ax2+2ax+c(a>0,c<0),与x轴交于A、B两点(A在B左侧),与y轴交于点C,A点坐标为(﹣3,0),抛物线顶点为D,△ACD的面积为3.
(1)求二次函数解析式;
(2)点P(m,n)是抛物线第三象限内一点,P关于原点的对称点Q在第一象限内,当QB2取最小值时,求m的值.
【答案】(1)抛物线的解析式为y=x2+2x﹣3.(2)当QB2取最小值时,m的值为﹣1﹣![]() .
.
【解析】
(1)根据S△ACD=S△AOD+S△OCD﹣S△AOC构建方程即可解决问题;
(2)构建二次函数,利用二次函数的性质即可解决问题;
解:(1)把A(﹣3,0)代入y=ax2+2ax+c得到c=﹣3a,
∴抛物线的解析式为y=ax2+2ax﹣3a=a(x+1)2﹣4a,
∴D(﹣1,﹣4a),C(0,﹣3a),
∵S△ACD=S△AOD+S△OCD﹣S△AOC,
∴![]() ×3×4a+
×3×4a+![]() ×3a×1﹣
×3a×1﹣![]() ×3×3a=15,
×3×3a=15,
解得a=1,
∴抛物线的解析式为y=x2+2x﹣3.
(2)由题意Q(﹣m,﹣n),B(1,0),
∴QB2=(m+1)2+n2,
∵n=(m+1)2﹣4,
∴(m+1)2=n+4,
∴QB2=n+4+n2=(n+![]() )2+
)2+![]() ,
,
∴n=﹣![]() 时,QB2有最小值,
时,QB2有最小值,
此时﹣![]() =(m+1)2﹣4,
=(m+1)2﹣4,
解得m=﹣1﹣![]() 或﹣1+
或﹣1+![]() (舍弃).
(舍弃).
∴当QB2取最小值时,m的值为﹣1﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出_____只粽子,利润为_____元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数![]() (k>0)有以下四个结论:
(k>0)有以下四个结论:
①这是y关于x的反比例函数;②当x>0时,y的值随着x的增大而减小;③函数图象与x轴有且只有一个交点;④函数图象关于点(0,3)成中心对称.
其中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A'B'C'D'及其内部的点,其中点A、B的对应点分别为A',B'.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F'与点F重合,则点F的坐标是( )
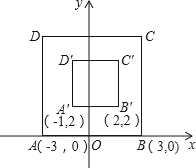
A. (1,4) B. (1,5) C. (﹣1,4) D. (4,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求证:无论m为任何实数,此函数图象与x轴总有两个交点;
(2)若此函数图象与x轴的一个交点为(-3,0),求此函数图象与x轴的另一个交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠B=90°,P是线段AB上的一个动点.
(1)若AD=2,BC=6,AB=8,且以A,D,P为顶点的三角形与以B,C,P为顶点的三角形相似,求AP的长;
(2)若AD=a,BC=b,AB=m,则当a,b,m满足什么关系时,一定存在点P使△ADP∽△BPC?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
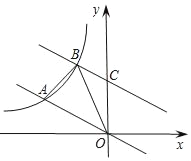
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() (k≠0)在第二象限内的图象相交于点A(m,1).
(k≠0)在第二象限内的图象相交于点A(m,1).
(1)求反比例函数的解析式;
(2)将直线y=﹣![]() x向上平移后与反比例函数图象在第二象限内交于点B,与y轴交于点C,且△ABO的面积为
x向上平移后与反比例函数图象在第二象限内交于点B,与y轴交于点C,且△ABO的面积为![]() ,求直线BC的解析式.
,求直线BC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:有一堵长为![]() 的墙,利用这堵墙和长为
的墙,利用这堵墙和长为![]() 的篱笆围成一个矩形养鸡场,怎样围面积最大?最大面积是多少?
的篱笆围成一个矩形养鸡场,怎样围面积最大?最大面积是多少?
题意理解:根据题意,有两种设计方案:一边靠墙(如图①)和一边“包含”墙(如图②).
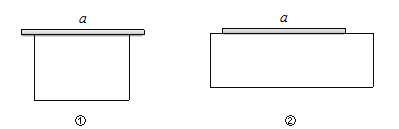
特例分析:
(1)当![]() 时,若按图①的方案设计,则该方案中养鸡场的最大面积是
时,若按图①的方案设计,则该方案中养鸡场的最大面积是 ![]() ;若按图②的方案设计,则该方案中养鸡场的最大面积是
;若按图②的方案设计,则该方案中养鸡场的最大面积是 ![]() .
.
(2)当![]() 时,解决“问题情境”中的问题.
时,解决“问题情境”中的问题.
解决问题:(3)直接写出“问题情境”中的问题的答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com