练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．能用平方差公式计算的是（　　）
    A．（-x+2y）（x-2y）B．（2x-y）（2y+x）C．（m-n）（n-m）D．99×101

    分析 只要符合两项的和与这两项的差的积的形式，才能运用平方差公式计算．

    解答 解：A、（-x+2y）（x-2y），因为-x与x、2y与-2y都是互为相反数，不符合平方差公式，所以不能运用平方差公式计算；
    B、（2x-y）（2y+x）=（2x-y）（x+2y），括号里的相同字母的两项的系数的绝对值相等，不符合平方差公式，所以不能运用平方差公式计算；
    C、（m-n）（n-m）=（m-n）（-m+n），因为m与-m、-n与n都是互为相反数，不符合平方差公式，所以不能运用平方差公式计算；
    D、99×101=（100-1）（100+1）=1002-12=10000-1=9999，符合平方差公式，所以能运用平方差公式计算；
    故选D．

    点评 本题考查平方差公式，符合两项的和与这两项的差的积的形式，才能运用平方差公式进行计算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．如图，在?ABCD中，点E、F分别在AD、BC上，且AE=CF，EF、BD相交于点O，求证：OE=OF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费y（元）是行李质量x（kg）的一次函数．已知行李质量为20kg时需付行李费2元，行李质量为50kg时需付行李费8元．
    （1）当行李的质量x超过规定时，求y与x之间的函数表达式；
    （2）求旅客最多可免费携带行李的质量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

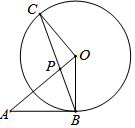    17．如图，AB与⊙O相切于点B，BC为⊙O的弦，OC⊥OA，OA与BC相交于点P．
    （1）求证：AP=AB；
    （2）若OB=4，AB=3，求线段BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．代数式$\frac{1}{4}$a的值不小于$\frac{1}{2}$a+1的值，则a应满足（　　）
    A．a≤4B．a≥4C．a≤-4D．a≥-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．学生问老师多少岁了，老师说：我和你这么大时，你才4岁，你到我这么大时，我就37岁了，则老师比学生大（　　）
    A．8岁B．9岁C．10岁D．11岁

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

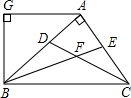    2．如图，AB⊥AC，AG⊥BG，CD、BE分别是∠ACB，∠ABC的角平分线，AG∥BC，下列结论：①∠BAG=2∠ABF；②BA平分∠CBG；③∠ABG=∠ACB；④∠CFB=135°、其中正确的结论是（　　）
    A．①③B．②④C．①③④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

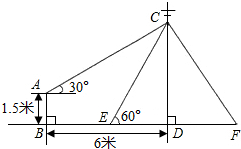    19．如图，在电线杆CD上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED=60°，在离电线杆6米的B处安置高为1.5米的测角仪AB，在A处测得电线杆上C处的仰角为30°，则拉线CE的长为（　　）（结果保留小数点后一位，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）．
    A．5.4B．5.7C．6.1D．6.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

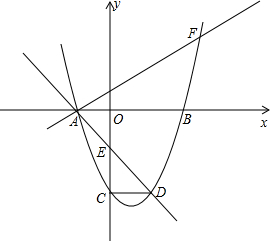    20．如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+bx-5与x轴交于A、B两点（点A在点B的左侧），与y轴交点为C，直线y=-x-2经过点A，交抛物线于点D，交y轴于点E，连接CD，并且∠ADC=45°．
    （1）求抛物线的解析式；
    （2）过点A的直线AF与抛物线的另一个交点为F，sin∠BAF=$\frac{\sqrt{5}}{5}$，求点F的坐标；
    （3）在（2）的条件下，点P是直线AF下方抛物线上一点，过点P作PQ⊥AF垂足为Q，若PE=EQ，求点P的坐标．

    查看答案和解析>>

    同步练习册答案