
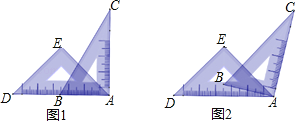
【题目】一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使BC边与三角形ADE的一边互相平行.则∠BAD(0°<∠BAD<180°)所有可能符合条件的度数为________________.
【答案】15O,60O,105O
【解析】(1)根据已知分三种情况(如图):利用两直线平行同位角相等,并求得∠BAD=45°-30°=15°;根据两直线平行内错角相等,得∠BAD=∠B=60 o;∠BAD=∠DAE+∠BAE=45 o +60 o=105 o.
(2)利用平行线的性质及旋转不变量求得旋转角即可.
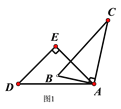
如图1,当BC∥DE时,
∠BAD=∠DAE-∠BAE=∠DAE-(90 o -∠B)=45 o -(90 o- 60 o)=15 o.
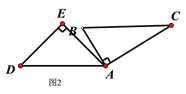
如图2,当BC∥AD时,
∠BAD=∠B=60 o.
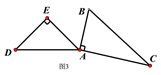
如图3,当BC∥AE时,
∠BAD=∠DAE+∠BAE=45 o +60 o=105 o.
故正确答案为:15°,60°,105°


科目:初中数学 来源: 题型:
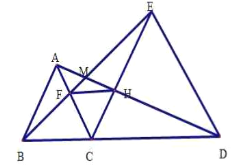
【题目】如图,已知△ABC和△ECD都是等边三角形,B、C、D在一条直线上。
求证:(1)BE=AD;
(2) △FCH是等边三角形
(3)求∠EMD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
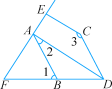
【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)请你判断DA与CE的位置关系,并说明理由;
(2)若DA平分∠BDC,CE⊥AE于E,∠1=70°,试求∠FAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( ).
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
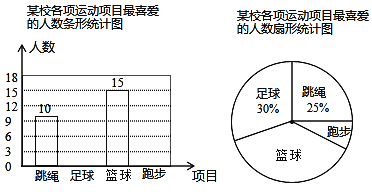
【题目】某中学积极开展“阳光体育”活动,共开设了跳绳、乒乓球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)根据统计的数据估计该中学3200名学生中最喜爱篮球的人数约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,购进 4 件甲种商品比购进 5 件乙种商品少用 10 元,购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
(1)求甲、乙两种商品每件进价分别是多少元?
(2)若该商店购进甲、乙两种商品共 140 件,都标价 10 元出售,售出一部分降价促销, 以标价的八折售完所有剩余商品,以 10 元售出的商品件数比购进甲种商品件数少 20 件,该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元,求至少购进甲种商品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com