

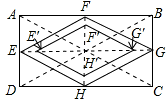
 解:连接AC、BD,
解:连接AC、BD, BD,
BD, BQ,EH=
BQ,EH= AC=FG,
AC=FG, ×80×60+
×80×60+ ×60×45,
×60×45,

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
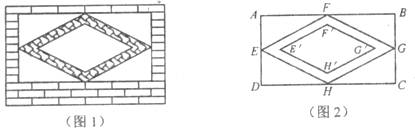
公园的风景墙上设计了一种矩形窗户(如图1),在矩形窗框内有等宽的四边形窗格(空白处用以通风透光).图2是其设计图,已知AD=60cm,AB=80cm,E、F、G、H分别是矩形各边的中点,四边形EFGH和E’F’G’H’形状相同.点E、E’、G’、G和F、F’、H’、H各在一条直线上,量得EE’=GG’=10cm,FF’=HH’=7.5cm.求窗户用以通风的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com