
已知:如图一次函数y= x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.
x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.
点D的坐标为(0,8);点E的坐标为(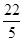 ,﹣
,﹣ ).
).
解析试题分析: 先求出点A坐标为(6,0),点B坐标为(0,﹣3),由于DE⊥AB,则∠AEC=90°,利用等角的余角相等得到∠ODC=∠EAC,易证得Rt△ODC∽Rt△OAB,得到OD:OA=OC:OB,即OD:6=4:3,
可求出OD=8,得到点D的坐标为(0,8);然后利用待定系数法求出直线CD的解析式为y=﹣2x+8,再解由y= x﹣3和y=﹣2x+8的方程组即可得到点E坐标.
x﹣3和y=﹣2x+8的方程组即可得到点E坐标.
试题解析:对于y=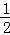 x﹣3,令x=0,则y=﹣3;令y=0,x=6,
x﹣3,令x=0,则y=﹣3;令y=0,x=6,
∴点A坐标为(6,0),点B坐标为(0,﹣3),
∵DE⊥AB,
∴∠AEC=90°,
∴∠ODC=∠EAC,
∴Rt△ODC∽Rt△OAB,
∴OD:OA=OC:OB,即OD:6=4:3,
∴OD=8,
∴点D的坐标为(0,8);
设过CD的直线解析式为y=kx+8,将C(4,0)代入得0=4k+8,解得k=﹣2,
∴直线CD的解析式为y=﹣2x+8,
解方程组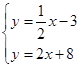 得
得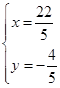 .
.
∴点E的坐标为(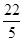 ,﹣
,﹣ ).
).
考点:两条直线相交或平行问题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
如图①是一个长方形ABCD,点P按B→C→D→A方向运动,开始时,以每秒2个单位长度匀速运动,到达C点后,改为每秒a个单位匀速运动,到达D后,改为每秒b个单位匀速运动,在整个运动过程中,三角形ABP的面积S与运动时间t的函数关系如图所示。
求:
(1)AB、BC的长;
(2)a,b的值。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a﹣5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A、C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y= (x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(1)求反比例函数的解析式和点D的坐标;
(2)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,这是反映爷爷每天晚饭后从家中出发去元宝山公园锻炼的时间与距离之间关系的一幅图.
(1)右图反映的自变量、因变量分别是什么?
(2)爷爷每天从公园返回用多长时间?
(3)爷爷散步时最远离家多少米?
(4)爷爷在公园锻炼多长时间?
(5)计算爷爷离家后的2 0分钟内的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com