
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
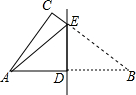 如图,在△ABC中,∠ACB=90°,DE⊥AB于点D,交BC边于点E,将△ABC沿直线DE折叠,点B恰好落在点A处,若AB=5,AC=3,则△ACE的周长为7.
如图,在△ABC中,∠ACB=90°,DE⊥AB于点D,交BC边于点E,将△ABC沿直线DE折叠,点B恰好落在点A处,若AB=5,AC=3,则△ACE的周长为7.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.05 | B. | 0.95 | C. | 1 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A(a,b)是双曲线y=$\frac{8}{x}$(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.
如图,点A(a,b)是双曲线y=$\frac{8}{x}$(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校需要置换一批推拉式黑板,经了解,现有甲、乙两厂家报价均为200元/米2,且提供的售后服务完全相同,为了促销,甲厂家表示,每平方米都按七折计费;乙厂家表示,如果黑板总面积不超过20米2,每平方米都按九折计费,超过20米2,那么超出部分每平方米按六折计费.假设学校需要置换的黑板总面积为x米2.
某学校需要置换一批推拉式黑板,经了解,现有甲、乙两厂家报价均为200元/米2,且提供的售后服务完全相同,为了促销,甲厂家表示,每平方米都按七折计费;乙厂家表示,如果黑板总面积不超过20米2,每平方米都按九折计费,超过20米2,那么超出部分每平方米按六折计费.假设学校需要置换的黑板总面积为x米2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com