
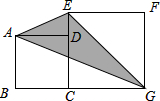
 已知如图,在线段BG同侧作正方形ABCD和正方形CEFG,其中BG=10,BC:CG=2:3,则S△ECG=
已知如图,在线段BG同侧作正方形ABCD和正方形CEFG,其中BG=10,BC:CG=2:3,则S△ECG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市通州九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,在⊙O中,直径AB⊥CD于点E,连接BC.

(1)线段BC、BE、AB应满足的数量关系是 ;
(2)若点P是优弧 上一点(不与点C、A、D重合),连接BP与CD交于点G.
上一点(不与点C、A、D重合),连接BP与CD交于点G.
请完成下面四个任务:
①根据已知画出完整图形,并标出相应字母;
②在正确完成①的基础上,猜想线段BC、BG、BP应满足的数量关系是 ;
③证明你在②中的猜想是正确的;
④点P′恰恰是你选择的点P关于直径AB的对称点,那么按照要求画出图形后在②中的猜想仍然正确吗? ;(填正确或者不正确,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知如图,在线段BG同侧作正方形ABCD和正方形CEFG,其中BG=10,BC:CG=2:3,则S△ECG=________,S△AEG=________.
已知如图,在线段BG同侧作正方形ABCD和正方形CEFG,其中BG=10,BC:CG=2:3,则S△ECG=________,S△AEG=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com