
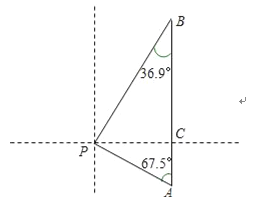
【题目】如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西36.9°方向,求此时轮船所处位置B与城市P的距离?(参考数据:sin36.9°≈![]() ,tan36.9°≈
,tan36.9°≈![]() ,sin67.5°≈
,sin67.5°≈![]() ,tan67.5°≈
,tan67.5°≈![]() )
)
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用普查方式的是( )
A. 调查全国中学生心理健康现状
B. 调查一片试验田里五种大麦的穗长情况
C. 要查冷饮市场上冰淇淋的质量情况
D. 调查你所在班级的每一个同学所穿鞋子的尺码情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由a+3=b变为2(a+3)-5=2b-5,其过程中所用等式的性质及顺序是( )
A. 先用等式的性质1,再用等式的性质2
B. 先用等式的性质2,再用等式的性质1
C. 仅用了等式的性质1
D. 仅用了等式的性质2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
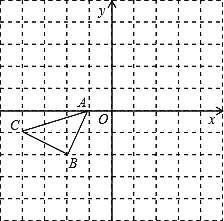
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P.若点P向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
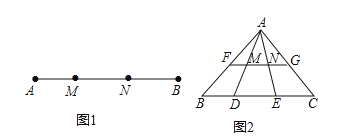
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )
A. y=(x﹣1)2+2 B. y=(x﹣1)2+3
C. y=(x﹣2)2+2 D. y=(x﹣2)2+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com