
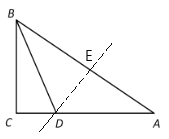
【题目】△ABC中,∠ACB=90°,CB=6,AC=8,点D是AC上的一点,点E是BD上一点.
(1)如图(1),若点D在AB的垂直平分线上,求CD的长.
(2)如图(2),连接AE,若AE平分∠BAC,BE平分∠ABC,求点E到AC的距离.
(3)若点E到三角形两边的距离为1.5,求CD的长.(直接写出答案)

【答案】(1)![]() (2)2(3)3或2或
(2)2(3)3或2或![]()
【解析】
(1)由垂直平分线的性质可得BD=AD,AE=BE=5,设CD长为x,在![]() 中,由勾股定理列出方程即可解出CD的长;
中,由勾股定理列出方程即可解出CD的长;
(2)过点E作EF⊥AC于点F,EM⊥AB于点M,EN⊥BC于点N,由角平分线的性质可得EF=EM=EN,AE、BE、CE将![]() 分割成三个三角形,利用面积关系
分割成三个三角形,利用面积关系![]() =
= ![]() 可求出EF的长即为所求;
可求出EF的长即为所求;
(3)根据题意可分三种情况讨论:①当点E到AB和BC的距离为1.5时,过点D作DF⊥AB于点F,设CD为x,在![]() 中利用勾股定理可列出方程,求出x;②当点E到CB和CA的距离为1.5时,过点E作EM⊥AC于点M,EN⊥BC于点N,易知四边形CMEN为正方形,可得CM=1.5,由EM∥BC,可得
中利用勾股定理可列出方程,求出x;②当点E到CB和CA的距离为1.5时,过点E作EM⊥AC于点M,EN⊥BC于点N,易知四边形CMEN为正方形,可得CM=1.5,由EM∥BC,可得![]() ,进而得到
,进而得到![]() ,代入数据即可求出CD;③当点E到AB和AC的距离为1.5时,过点E作EM⊥AB于点M,EN⊥AC于点N,EF⊥BC于点F,易知四边形CNEF为矩形,根据面积关系
,代入数据即可求出CD;③当点E到AB和AC的距离为1.5时,过点E作EM⊥AB于点M,EN⊥AC于点N,EF⊥BC于点F,易知四边形CNEF为矩形,根据面积关系![]() =
= ![]() 可求EF的长度即为CN的长度,由EN∥BC,可得
可求EF的长度即为CN的长度,由EN∥BC,可得![]() 进而可得
进而可得![]() ,代入数据即可求出CD的长度.
,代入数据即可求出CD的长度.
(1)如图所示,设AB的垂直平分线为DE,垂足为E,
∵∠ACB=90°,CB=6,AC=8,
∴AB=![]() =10,
=10,
∵DE垂直平分AB,
∴BD=AD,AE=BE=![]() AB=5,
AB=5,
设CD=x,则AD=BD=8-x,在![]() 中,由勾股定理可得:
中,由勾股定理可得:
![]() ,
,
解得:![]() ,
,
∴点D在AB的垂直平分线上时,CD= ![]() ;
;
(2)如图所示,过点E作EF⊥AC于点F,EM⊥AB于点M,EN⊥BC于点N,连接CE,

∵AE平分∠BAC,EF⊥AC,EM⊥AB,
∴EF=EM,
∵BE平分∠ABC,EM⊥AB,EN⊥BC,
∴EM=EN,
∴EF=EM=EN,
设EF=EM=EN=x,则:
![]() =
= ![]()
即:![]() ×AC×BC=
×AC×BC= ![]() ×AC×EF+
×AC×EF+ ![]() ×AB×EM+
×AB×EM+ ![]() ×BC×EN,
×BC×EN,
6×8=8x+10x+6x,
解得:x=2,
∴点E到AC的距离为2;
(3)根据题意可分三种情况:
①如图所示,当点E到AB和BC的距离为1.5时,此时点E在∠CBA的角平分线上,即BD平分∠CBA,过点D作DF⊥AB于点F,

∵BD平分∠CBA,DF⊥AB,DC⊥BC,
∴CD=DF,
又∵∠C=∠DFB=90°,BD=BD,
∴![]() (HL),
(HL),
∴BF=BC=6,
∴AF=4,
设CD=x,则DF=x,AD=8-x,在![]() 中,由勾股定理可得:
中,由勾股定理可得:
![]() ,
,
解得:x=3,
∴当点E到AB和BC的距离为1.5时,CD=3;
②如图所示,当点E到CB和CA的距离为1.5时,此时点E在∠BCA的角平分线上,即CE平分∠BCA,过点E作EM⊥AC于点M,EN⊥BC于点N,此时EM=EN=1.5,EM∥BC,

∵∠NCM=90°, EM⊥AC,EN⊥BC,
∴四边形CMEN为矩形,
∵EM=EN
∴矩形CMEN为正方形,
∴CM=1.5,
设CD=x,则DM=x-1.5,
∵EM∥BC,
∴![]()
∴![]() ,
,
即: ![]() ,
,
解得:x=2,
∴当点E到CB和CA的距离为1.5时,CD=2;
③如图所示,当点E到AB和AC的距离为1.5时,此时点E在∠BAC的角平分线上,即AE平分∠BAC,过点E作EM⊥AB于点M,EN⊥AC于点N,EF⊥BC于点F,此时EM=EN=1.5,四边形CNEF为矩形,

∵![]() =
= ![]() ,
,
∴![]() ×AC×BC=
×AC×BC= ![]() ×AC×EN+
×AC×EN+ ![]() ×AB×EM+
×AB×EM+ ![]() ×BC×EF,
×BC×EF,
即6×8=8×1.5+10×1.5+6×EF,
解得:EF=![]() ,
,
∵四边形CNEF为矩形,
∴CN= EF=![]() ,
,
设CD=x,则DN=x-![]() ,
,
∵EN∥BC,
∴![]()
∴![]() ,
,
即: 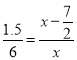 ,
,
解得:x=![]() ,
,
∴当点E到AB和AC的距离为1.5时,CD= ![]() .
.
综上所述,若点E到三角形两边的距离为1.5,CD的长为3或2或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练.物理、化学各有3个不同的操作实验题目,物理用番号①、②、③代表,化学用字母a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.
(1)小张同学对物理的①、②和化学的b、c实验准备得较好.请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率;
(2)小明同学对物理的①、②、③和化学的a实验准备得较好.他两科都抽到准备得较好的实验题目的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3![]() ).动点P从A点开始沿折线AO﹣OB﹣BA运动,点P在AO,OB,BA上运动,速度分别为1,
).动点P从A点开始沿折线AO﹣OB﹣BA运动,点P在AO,OB,BA上运动,速度分别为1,![]() ,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以
,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以![]() (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO﹣OB﹣BA运动一周时,直线l和动点P同时停止运动.
(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO﹣OB﹣BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:
(1)过A,B两点的直线解析式是 ,∠BAO= ;
(2)当t﹦4时,点P的坐标为 ;当t﹦ ,点P与点E重合;
(3)作点P关于直线EF的对称点P′.在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=BC=12cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.

(1)求证:△BMD为等腰直角三角形.
(2)当点E运动3秒时,求△BMD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数![]() 和
和![]() 的图象分别为直线
的图象分别为直线![]() ,
,![]() ,过点(1,0)作
,过点(1,0)作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,…依次进行下去,则点
,…依次进行下去,则点![]() 的坐标为_________.
的坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )

A. 10 B. 12 C. 15 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD,且AD=4,点P为线段AC上一动点,连接BP.则2BP+AP的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E到△ABC三边的距离相等,过点E作MN∥BC交AB于M,交AC于N.若BM+CN=2019,则线段NM的长为( )

A.2017B.2018C.2019D.2020
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com