
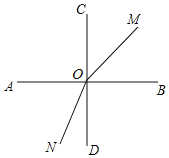
【题目】如图,两条直线AB、CD相交于点O,且∠AOC=90°,射线OM从OB开始绕O点逆时针方向旋转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s.两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
(1)当t=2时,∠MON的度数为 ,∠BON的度数为 ;∠MOC的度数为
(2)当0<t<12时,若∠AOM=3∠AON-60°,试求出t的值;
(3)当0<t<6时,探究![]() 的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?

【答案】(1)144°,114°,60°;(2)t的值为![]() 秒或10秒;(3)当0<t<
秒或10秒;(3)当0<t<![]() 时,
时,![]() 的值不是定值;当
的值不是定值;当![]() <t<6时,
<t<6时,![]() 的值是3.
的值是3.
【解析】
(1)根据时间和速度分别计算∠BOM和∠DON的度数,再根据角的和与差可得结论;
(2)分两种情况:①如图所示,当0<t≤7.5时,②如图所示,当7.5<t<12时,分别根据已知条件列等式可得t的值;
(3)分两种情况,分别计算∠COM、∠BON和∠MON的度数,代入可得结论.
(1)由题意得:∠MON=∠BOM+∠BOD+∠DON=2×15°+90°+2×12°=144°,
∠BON=∠BOD+∠DON=90°+24°=114°,
∠MOC=∠BOC-∠BOM=90°-2×15°=60°,
故答案为:144°,114°,60°;
(2)当ON与OA重合时,t=90÷12=7.5(s)
当OM与OA重合时,t=180°÷15=12(s)
①如图所示,当0<t≤7.5时,∠AON=90°-12t°,∠AOM=180°-15t°
由∠AOM=3∠AON-60°,可得180-15t=3(90-12t)-60,
解得t=![]() ,
,
②如图所示,当7.5<t<12时,∠AON=12t°-90°,∠AOM=180°-15t°,
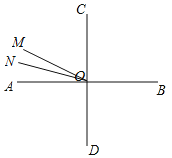
由∠AOM=3∠AON-60°,可得180-15t=3(12t-90)-60,解得t=10,
综上,t的值为![]() 秒或10秒;
秒或10秒;
(3)当∠MON=180°时,∠BOM+∠BOD+∠DON=180°,
∴15t+90+12t=180,解得t=![]() ,
,
①如图所示,当0<t<![]() 时,∠COM=90°-15t°,∠BON=90°+12t°,
时,∠COM=90°-15t°,∠BON=90°+12t°,
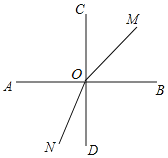
∠MON=∠BOM+∠BOD+∠DON=15t°+90°+12t°,
∴![]() (不是定值),
(不是定值),
②如图所示,当![]() <t<6时,∠COM=90°-15t°,∠BON=90°+12t°,
<t<6时,∠COM=90°-15t°,∠BON=90°+12t°,
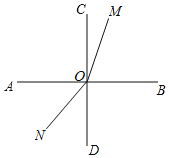
∠MON=360°-(∠BOM+∠BOD+∠DN)=360°-(15t°+90°+12t°)=270°-27t°,
∴![]() =3(定值),
=3(定值),
综上所述,当0<t<![]() 时,
时,![]() 的值不是定值;当
的值不是定值;当![]() <t<6时,
<t<6时,![]() 的值是3.
的值是3.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】下列说法:①绝对值不大于![]() 的所有整数的和为零,积也为零;②n个有理数相乘,若有奇数个负因数,积必为负数;③
的所有整数的和为零,积也为零;②n个有理数相乘,若有奇数个负因数,积必为负数;③![]() ;④如果一个有理数小于1,那么这个数的平方一定小于原数,不正确的有( )
;④如果一个有理数小于1,那么这个数的平方一定小于原数,不正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
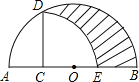
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民王先生上周星期五买进某公司股票1000股,每股18元,本周该股票的涨跌情况如表(正数表示价格比前一天上涨,负数表示价格比前一天下跌,单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
(1)星期三结束时,该股票每股多少元?
(2)该股票本周内每股的最高价和最低价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3.
(1)若函数图象经过点(1,﹣4),(﹣1,0),求a,b的值;
(2)证明:若2a﹣b=1,则存在一条确定的直线始终与该函数图象交于两点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产______辆.
(2)产量最多的一天比产量最少的一天多生产_______辆.
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
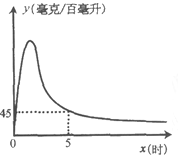
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com