[题目]点A在数轴上和原点相距3个单位长度.点B在数轴上和原点相距个单位长度.则A.B两点这间的距离是．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】点A在数轴上和原点相距3个单位长度，点B在数轴上和原点相距个单位长度，则A、B两点这间的距离是．

【答案】3+ 或3﹣
【解析】解：设点A表示a，点B表示b，

∵A在数轴上和原点相距3个单位长度，点B在数轴上和原点相距个单位长度，

∴a=±3，b=± ，

∴当a=3，b= 时，

∴AB=|3﹣ |=3﹣ ；

当a=﹣3，b= 时，

∴AB=|﹣3﹣ |=3+ ；

当a=﹣3，b= 时，

∴AB=|﹣3﹣ |=3+ ；

当a=﹣3，b=﹣ 时，

∴AB=|﹣3+ |=3﹣ ；

所以答案是：3+ 或3﹣ ．

【考点精析】利用实数与数轴的关系对题目进行判断即可得到答案，需要熟知实数与数轴上的点一一对应．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

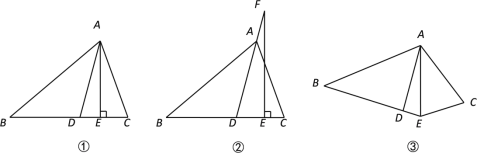
【题目】如图①，平分，⊥，∠B=450,∠C=730．

（1）求的度数；

（2）如图②，若把“⊥”变成“点F在DA的延长线上，”，其它条件不变，求的度数；

（3）如图③，若把“⊥”变成“平分”，其它条件不变，的大小是否变化，并请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知在平面直角坐标系中，∠2＝2∠1，点C为x轴正半轴上的一动点．

（1）求∠1的度数；

（2）若OF∥AC，OE∥AB，求证：∠EOF＝∠EAF；

（3）点C在运动中，若∠1＝∠ACO，试判断AB与AC有怎样的位置关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．

求证：AF平分∠BAC．

【答案】证明见解析.

【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．

试题解析：证明：∵AB=AC(已知)，

∴∠ABC=∠ACB(等边对等角).

∵BD、CE分别是高，

∴BD⊥AC,CE⊥AB(高的定义).

∴∠CEB=∠BDC=90°.

∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.

∴∠ECB=∠DBC(等量代换).

∴FB=FC(等角对等边)，

在△ABF和△ACF中，

，

∴△ABF≌△ACF(SSS)，

∴∠BAF=∠CAF(全等三角形对应角相等)，

∴AF平分∠BAC.

【题型】解答题
【结束】
23

【题目】如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E．

（1）求证：CD=BE；

（2）已知CD=2，求AC的长；

（3）求证：AB=AC+CD．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是（）
A. =
B. =
C. =
D. =

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，一次函数y=kx+3分别与x，y轴交于点N，M，与反比例函数y= （x＞0）的图象交于点A，若AM：MN=2：3，则k= ．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图，斜坡AP的坡度为1：2.4，坡长AP为26米，在坡顶A处的同一水平面上有一座古塔BC，在斜坡底P处测得该塔的塔顶B的仰角为45°，在坡顶A处测得该塔的塔顶B的仰角为76°．求：

（1）坡顶A到地面PQ的距离；
（2）古塔BC的高度（结果精确到1米）．（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）