
����Ŀ����ͼ1����ABC�͡�CDE���ǵȱ������Σ��ҵ�A��C��E��һ��ֱ���ϣ�AD��BE���ڵ�O��AD��BC���ڵ�P��CD��BE���ڵ�Q������PQ
��1����֤��AD��BE��
��2����AOB�Ķ���Ϊ�� ����PQ��AE��λ�ù�ϵ���� ����
��3����ͼ2����ABC�̶�������CDE�Ƶ�C��˳ʱ�루����ʱ�룩������ת����Ƕ���������ת�����У���1���еĽ����Ƿ��ܳ�������AOB�Ķ����Ƿ�ı䣿��˵�����ɣ�

���𰸡���1������������2��60�㣬PQ��AE����3������ת�����У���1���еĽ����ܳ�������AOB�Ķ�������ı䣬������
��������
��1�����ݵȱ����������ʵó�AC��BC��CE��CD����ACB����ECD��60���������BCE����ACD������SAS�Ƴ���������ȫ�ȼ��ɣ�
��2���������ε�������ʣ��ɵá�AOB����BEA+��DAC����ACB����EBC+��BEA�����AOB����ACB��60����֤����QPC����BCA���ɵ�PQ��AE��
��3��֤����ACD�ա�BCE��SAS�����õ�AD��BE����DAC����EBC�����ݡ�BOA��180������ABO����BAO��180������ABC����BAC�����ɽ��
��1��֤�����ߡ�ABC�͡�CDEΪ�ȱ������Σ�
��AC��BC��CD��CE����BCA����DCE��60����
���ACD����BCE��
�ڡ�ACD�͡�BCE�У�
AC��BC����ACD����BCE��CD��CE��
���ACD�ա�BCE��SAS����
��AD��BE��
��2���ߡ�ACD�ա�BCE��
���DAC����EBC��
�������ε�������ʣ���AOB����BEA+��DAC��
��ACB����EBC+��BEA��
���AOB����ACB��60����
�ߡ�DCP��60������ECQ��
���ڡ�CDP�͡�CEQ�У�
��ADC����BEC��CD��CE����DCP����ECQ��
���CDP�ա�CEQ��ASA����
��CP��CQ��
���CPQ����CQP��60������PCQ�ǵȱ������Σ�
���QPC����BCA��
��PQ��AE��
�ʴ�Ϊ��60����PQ��AE��
��3������ת�����У���1���еĽ����ܳ�������AOB�Ķ�������ı䣬�������£�
�ߡ�ABC�͡�CDE���ǵȱ������Σ�
��AC��BC��CD��CE����ACB����DCE��60����
���ACB+��BCD����DCE+��BCD��
����ACD����BCE��
�ڡ�ACD�͡�BCE�У�
��AC=BC����ACD=��BCE��CD=CE��
���ACD�ա�BCE��SAS����
��AD��BE����DAC����EBC��
���BOA��180������ABO����BAO��180������ABC����BAC��60����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵĵ�A��B��C��D��E��ʾ�����������������Ӧ���ֱ�Ϊa��b��c��d��e��
![]()
��1����a+e=0�������ʽb+c+d=������
��2����a����С�����������Ȼ�������ֵ��![]() ��
��
��3����a+b+c+d=2�������ϵĵ�M��ʾ��ʵ��Ϊm��m��a��b��c��d��e��ͬ����������MA+MD=3����m�ķ�Χ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
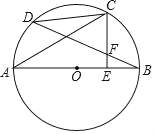
����Ŀ����ͼ��AB����O��ֱ������C�ǻ�BD���е㣬CE��AB�ڵ�F��
��1����֤��BF=CF��
��2����CD=3cm��AC=4cm������O�İ뾶��CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����
����![]() ��
�У�![]() ��ԭ�㣬
��ԭ�㣬![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�
![]() ȷ��
ȷ��![]() ����ֱ�ߵĺ�������ʽ;
����ֱ�ߵĺ�������ʽ;
![]() ���߶�
���߶�![]() ���Ƿ���һ��
���Ƿ���һ��![]() ,ʹ��
,ʹ��![]() ��
��![]() ���
���![]() ��ľ�����ȣ������ڣ����
��ľ�����ȣ������ڣ����![]() �������;�������ڣ���˵������;
�������;�������ڣ���˵������;
![]() ���߶�
���߶�![]() ���Ƿ���һ��
���Ƿ���һ��![]() ,ʹ��
,ʹ��![]() ����
����![]() �͵�
�͵�![]() �ľ�����ȣ������ڣ�ֱ��д����
�ľ�����ȣ������ڣ�ֱ��д����![]() ������;�������ڣ���˵�����ɣ�
������;�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣���ͬһƽ��ֱ������ϵ�У�����y=ax2+bx��y=bx+a��ͼ������ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��9�£�ij�ֻ���˾�������¿������ֻ���Ϊ�˵���ijС��ҵ���Ըÿ��ֻ��Ĺ������ù�˾��ijС������Բ���ҵ���������ʾ����飬�涨ÿ��ֻ�ܴ�A�ࣨ����ȥ��������B�ࣨ���ۺ���ȥ��C�ࣨ��ԥ�У���D�ࣨ�϶�������������ѡһ�࣬���Ƴ�������������������ͳ��ͼ����ͼ������������Ϣ����������⣺
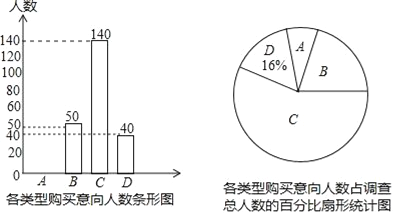
��1������ͳ��ͼ��B���Ӧ�İٷֱ�Ϊ�� ��%���벹ȫ����ͳ��ͼ��
��2������С������4000�ˣ�������Ƹ�С����Լ�ж���������ȥ�����ÿ��ֻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�����ʦ��ʾ�����¿��е���Ŀ��
�ڵȱ�������ABC�У���E��AB�ϣ���D��CB���ӳ����ϣ���ED=EC����ͼ����ȷ���߶�AE��DB�Ĵ�С��ϵ����˵�����ɣ� |
|
С����ͬ��С�����ۺ��������½��
��1�����������̽������
����EΪAB���е�ʱ����ͼ1��ȷ���߶�AE���DB��С��ϵ������ֱ��д�����ۣ�
AE DB(�����������������)��

ͼ1 ͼ2
��2�����������������Ŀ
�⣺��Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ�AE DB(�����������������)��
�������£���ͼ2������E��EF��BC����AC�ڵ�F.
(����������½�����)
��3����չ���ۣ��������
�ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED=EC������ABC�ı߳�Ϊ1��AE=2����CD�ij�(����ֱ��д�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
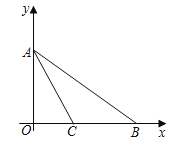
����Ŀ����ͼ����ֱ֪��y=kx+b��x���ڵ�A����y���ڵ�B��ֱ��y=2x��4��x���ڵ�D����ֱ��AB�ཻ�ڵ�C��3��2����
��1������ͼ��д������x�IJ���ʽ2x��4��kx+b�Ľ⼯��
��2������A������Ϊ��5��0������ֱ��AB�Ľ���ʽ��
��3���ڣ�2���������£����ı���BODC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������8�֣�ij�̼�Ԥ��һ��Ӧ�������ܳ����г�������13200Ԫ������һ�����ֳ��������к��Ȼ����Ӧ���̼�����28800Ԫ�����˵ڶ������ֳ��������������ǵ�һ����������2���������۹���10Ԫ��
��1�����̼ҹ����ĵ�һ�������Ƕ��ټ���
��2����������������ͬ�ı�����ۣ����ʣ��50���������Ż������������������ȫ������������ʲ�����25%���������������أ�����ôÿ�������ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com