练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    反比例函数y=的图象经过点A(4,-2),
    (1)求这个函数的解析式;
    (2)请判断点B(1,8)是否在这个反比例函数的图象上,并说明理由.

    (1)y=-.   (2)不在.

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如图，直线y=x﹣1与反比例函数y=的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（﹣1，m）．
    ⑴求反比例函数的解析式；
    ⑵若点P（n，1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．
    ⑶若B（2,1），当x为何值时，一次函数的值大于反比例函数的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知反比例函数y=的图象与正比例函数y=kx的图象交于点A（m，﹣2）．
    （1）求正比例函数的解析式及两函数图象另一个交点B的坐标；
    （2）试根据图象写出不等式≥kx的解集；
    （3）在反比例函数图象上是否存在点C，使△OAC为等边三角形？若存在，求出点C的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图所示，制作某种食品的同时需将原材料加热，设该材料温度为y ℃，从加热开始计算的时间为x分钟.据了解，该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃，加热一段时间使材料温度达到28℃时停止加热，停止加热后，材料温度逐渐下降，这时温度y与时间x成反比例函数关系，已知当第12分钟时, 材料温度是14℃.
    （1）分别求出该材料加热和停止加热过程中y与x的函数关系式（写出x的取值范围）；
    （2）根据该食品制作要求，在材料温度不低于12℃的这段时间内，需要对该材料进行特殊处理，那么对该材料进行特殊处理的时间为多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某乡要在生活垃圾存放区建一个老年活动中心，这样必须把1 200 m3的生活垃圾运走．
    (1)假如每天能运x m3，所需时间为y天，写出y与x之间的函数关系式；
    (2)若每辆拖拉机一天能运12 m3，则5辆这样的拖拉机要多少天才能运完？
    (3)在(2)的情况下，运了8天后，剩下的任务要在不超过6天的时间完成，那么至少需要增加多少辆这样的拖拉机才能按时完成任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知：如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为(2，m)，点B的坐标为(n，），tan∠BOC。

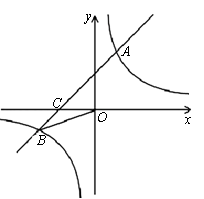
    （l）求该反比例函数和一次函数的解析式；
    （2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图,.是反比例函数(k>0)在第一象限图象上的两点,点的坐标为(2,0),若△与△均为等边三角形.

    （1）求此反比例函数的解析式；
    （2）求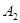点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线L经过点A（0，﹣1），且与双曲线c：交于点B（2，1）．

    （1）求双曲线c及直线L的解析式；
    （2）已知P（a﹣1，a）在双曲线c上，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    （2013年四川自贡4分）如图，在函数的图象上有点P1、P2、P3…、Pn、Pn+1，点P1的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn，则S1=
    　 　，Sn=　 　．（用含n的代数式表示）

    查看答案和解析>>

    同步练习册答案