
【题目】参照学习反比例函数的过程与方法,探究函数 y1=![]() (x≠0)的图象与性质,因为 y1=
(x≠0)的图象与性质,因为 y1=![]() =1﹣
=1﹣![]() ,即 y1=﹣
,即 y1=﹣![]() +1,所以我们对比函数 y=﹣
+1,所以我们对比函数 y=﹣![]() 来探究画出函数 y1=
来探究画出函数 y1=![]() (x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
(x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
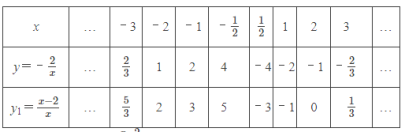
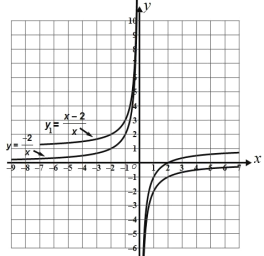
(1)观察:由 y1=![]() 图象可知:
图象可知:
①当 x>0 时,y 随 x的增大而 (填“增大”或“减小”)
②y1=![]() 的图象可以由 y=﹣
的图象可以由 y=﹣![]() 的图象向 平移 个单位长度得到.
的图象向 平移 个单位长度得到.
③y1 的取值范围是 .
(2)探究:①若直线 l 对应的函数关系式为 y2=kx+b,且经过点(﹣1,3)和点(1,﹣1),请再给出的平面直角坐标系中画出 y2,若 y1>y2,则 x 的取值范围为 .
②A(m1,n1),B(m2,n2)在函数 y=![]() 图象上,且 n1+n2=2,求 m1+m2 的值.
图象上,且 n1+n2=2,求 m1+m2 的值.
【答案】(1)①增大,②上,1,③y1≠1;(2)①-1<x<0或x>1,②![]() .
.
【解析】
(1)①②③观察图象即可解决问题;
(2)①根据点(﹣1,3)和点(1,﹣1)即可画出y2=kx+b的图象,可判断这两个点也经过y1=![]() 图象,所以根据图象即可判断y1>y2时x 的取值范围.
图象,所以根据图象即可判断y1>y2时x 的取值范围.
②分别将A、B两点代入y=![]() 中,由n1+n2=2可得出关于m1 、m2的等式,对等式进行变形即可得出m1+m2=0.
中,由n1+n2=2可得出关于m1 、m2的等式,对等式进行变形即可得出m1+m2=0.
(1)①当 x>0 时,y 随 x的增大而增大;
②向上平移1个单位得到;
③y1的取值范围为y1≠1;
(2)①因为函数y2=kx+ b经过点(﹣1,3)和点(1,﹣1),
所以其图象如下:
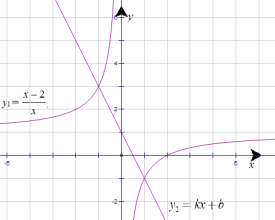
将x=-1代入y1=![]() ,可求得y1=3,所以点(﹣1,3)也在y1=
,可求得y1=3,所以点(﹣1,3)也在y1=![]() 上,
上,
将x=1代入y1=![]() ,可求得y1=-1,所以点(1,-1)也在y1=
,可求得y1=-1,所以点(1,-1)也在y1=![]() 上.
上.
所以根据图象,若y1>y2,则x的取值范围为-1<x<0或x>1.
②∵A(m1,n1),B(m2,n2)在函数 y=![]() 图象上
图象上
∴![]()
∵n1+n2=2
∴![]()
即![]()
即![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
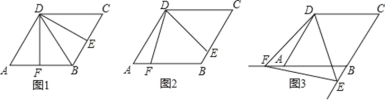
【题目】如图,四边形 ABCD 是边长为 2,一个锐角等于 60°的菱形纸片,将一个∠EDF=60°的三角形纸片的一个顶点与该菱形顶点 D 重合,按顺时针方向旋转这个三角形纸片,使它的两边分别交 CB,BA(或它们的延长线)于点 E, F;
①当 CE=AF 时,如图①,DE 与 DF 的数量关系是 ;
②继续旋转三角形纸片,当 CE≠AF 时,如图②,(1)的结论是否成立?若成立,加以证明;若不成立,请说明理由;
③再次旋转三角形纸片,当点 E,F 分别在 CB,BA 的延长线上时,如图③, 请直接写出 DE 与 DF 的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:
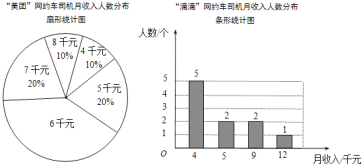
根据以上信息,整理分析数据如下:

(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣x﹣6.
(1)画出函数的图象;
(2)观察图象,指出方程x2﹣x﹣6=0的解及不等式x2﹣x﹣6>0解集;
(3)求二次函数的图象与坐标轴的交点所构成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中∠ACB=90°、∠CAB=30°,△ABD 是等边三角形将四边形 ACBD 折叠,使点 D 与点 C 重合,HK 为折痕,则cos∠ACH 的值是( )
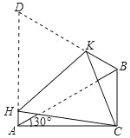
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的x,y的对应值如下表:

下列关于该函数性质的判断
①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com