
【题目】如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C,过点C作CD⊥AD于D,AB的延长线与DC的延长线相交于点P,∠ACB的角平分线CE交AB于点F、交⊙O于E.
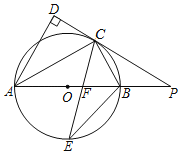
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图,连接OC,根据AC是∠DAB的角平分线,证明OC∥AD,进而可证PC与⊙O相切;
(2)根据CF是∠ACB的角平分线,和外角定义即可得∠PFC=∠PCF,进而得PC=PF;
(3)根据AB 是⊙O的直径,可得∠ACB=90°,根据AC=8,tan∠ABC=![]() =
=![]() ,可得BC=6,再根据勾股定理和垂径定理即可得线段BE的长.
,可得BC=6,再根据勾股定理和垂径定理即可得线段BE的长.
(1)如图,连接OC,
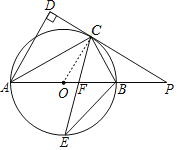
∵OA=OC,
∴∠OAC=∠OCA,
∵AC是∠DAB的角平分线,
∴∠DAC=∠OAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴PC与⊙O相切;
(2)∵CF是∠ACB的角平分线,
∴∠ACF=∠BCF,
∵∠CAF=∠PCB,
∴∠ACF+∠CAF=∠BCF+∠PCB,
∴∠PFC=∠PCF,
∴PC=PF.
(3)∵AB 是⊙O的直径,
∴∠ACB=90°,
∵AC=8,tan∠ABC=![]() =
=![]() ,
,
∴BC=6,
∴AB=![]() =10,
=10,
∴OB=OE=5,
∵∠ACE=∠BCE,
∴![]() ,
,
∴EO⊥AB,
∴BE=![]() =5
=5![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+(m﹣2)x+3(m+1)与x轴交于AB两点(A在B左侧),与y轴正半轴交于点C.
(1)当m≠﹣4时,说明这个二次函数的图象与x轴必有两个交点;
(2)若OAOB=6,求点C的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上找一点P,使S△PAC的面积为15,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
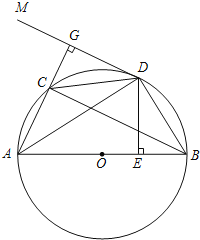
【题目】如图,AB是![]() 的直径,D是
的直径,D是![]() 的中点,
的中点,![]() 于E,交CB于点
于E,交CB于点![]() 过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
![]() 求证:GD是
求证:GD是![]() 的切线;
的切线;
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
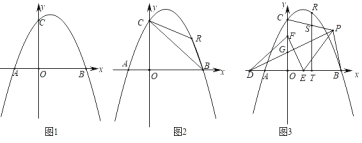
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D在边BC上,点E在线段AD上.
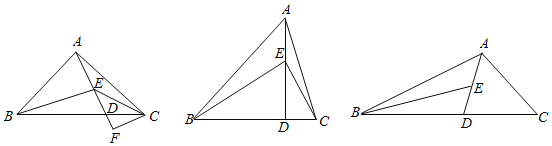
(1)若∠BAC=∠BED=2∠CED=α,
①若α=90°,AB=AC,过C作CF⊥AD于点F,求![]() 的值;
的值;
②若BD=3CD,求![]() 的值;
的值;
(2)AD为△ABC的角平分线,AE=ED=2,AC=5,tan∠BED=2,直接写出BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
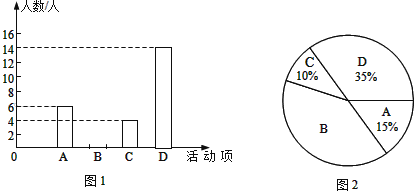
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
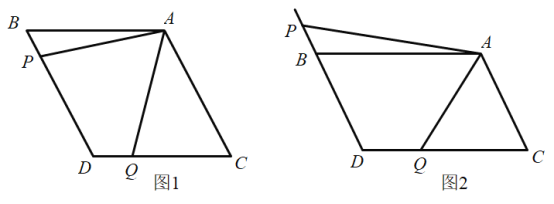
【题目】如图1,![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,且满足
上的点,且满足![]() .
.
(1)求证:![]()
(2)在图1中,是否存在与AP相等的线段?若存在,请找出来,并加以证明;若不存在,说明理由.
(3)若将“![]() 为
为![]() 上的点”改为:“
上的点”改为:“![]() 为DB延长线上的点”其他条件不变(如图2)若
为DB延长线上的点”其他条件不变(如图2)若![]() ,求线段
,求线段![]() 之间的数量关系(用含
之间的数量关系(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com