
����Ŀ�������ڵ�����ʵʩ������ƶ�����ߵĺ����£�������չ�Ƽ���ƶ�Ļ�ũ��ũ�������ڿƼ���Ա��ָ���£���������Ʒ�֣�ȥ�����ҵĸ���ϲ����գ���������ζ����������Ѷǰ���ɹ�����Э�̣��ɹ���y��Ԫ/�֣���ɹ���x���֣�֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ��
��2��������ֲ���ٵijɱ���800Ԫ/�֣������̲ɹ����Ƕ���ʱ��������������۸���ʱ���������������Ƕ��٣�
���𰸡�
��1���⣺��0��x��10ʱ��y=2000��
��10��x��20ʱ����BC����ĺ�����ϵʽΪy=kx+b��
�� ![]() ����ã�
����ã� ![]() ��
��
��y��x֮��ĺ�����ϵʽΪ��y=��80x+2800
��2���⣺��0��x��10ʱ�����Ż�õ�����Ϊ��
w=��2000��800��x
=1200x��12 000����ʱ���Ż�õ��������Ϊ12 000Ԫ��
��10��x��20ʱ�����Ż�õ�����Ϊw=����80x+2800��800��x
=��80��x2��25x��=��80��x��12.5��2+12500��
�൱x=12.5ʱ������wȡ�����ֵ�����ֵΪ12500Ԫ��
��12500��12 000��
�൱���̵IJɹ���Ϊ12.5��ʱ���������������������õ���������������Ϊ12500Ԫ
����������1������һ���ֶκ������ֱ���ݵ�0��x��10ʱ�͵�10��x��20ʱ�������Ӧ�ĺ�������ʽ��
��2���ȷֱ������0��x��10ʱ�͵�10��x��20ʱ��������x�ĺ�����ϵʽ���ٷֱ�����������ʱ��x��ֵ���ٱȽϴ�С���ɡ�
�����㾫����ͨ��������ö��κ�������ֵ����������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a�����Խ����⣮


 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD����A=110�㣬����D��AB��AC�Ĵ�ֱƽ�����ϣ����BDCΪ�� ��
A.90��
B.110��
C.120��
D.140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����λΪ1�ķ���ֽ�ϣ���A1A2A3 �� ��A3A4A5 �� ��A5A6A7 �� ������б����x���ϡ�б�߳��ֱ�Ϊ2��4��6�����ĵ���ֱ�������Σ�����A1A2A3�Ķ�������ֱ�ΪA1��2��0����A2��1����1����A3��0��0��������ͼ����ʾ���ɣ�A2017�ĺ�����Ϊ�� ��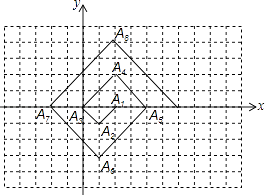
A.1010
B.2
C.1
D.��1006
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2��m+1��x+m2+2=0
��1����������ʵ��������ʵ��m��ȡֵ��Χ��
��2����������ʵ�����ֱ�Ϊx1��x2 �� ������x12+x22=10����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ĸ�ȫ�ȵ�ֱ�������ΰ�ͼʾ��ʽΧ��������ABCD�������ϳ�ֱ�DZߵ��е������ߣ�Χ�����Ϊ![]() ��С������EFGH����֪AMΪRt��ABM�ϳ�ֱ�DZߣ�AM=
��С������EFGH����֪AMΪRt��ABM�ϳ�ֱ�DZߣ�AM=![]() EF����������ABCD�����Ϊ�� ��
EF����������ABCD������� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E�ǡ�ABC�����ģ�AE���ӳ��ߺ͡�ABC�����Բ�ཻ�ڵ�D������BD��BE��CE������CBD=32�㣬���BEC�Ķ���Ϊ�� ��
A.128��
B.126��
C.122��
D.120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��N��P��G�ֱ��ڱ�AB��BC��CD��DA�ϣ���M��F��Q���ڶԽ���BD�ϣ����ı���MNPQ��AEFG��Ϊ�����Σ��� ![]() ��ֵ���� ��
��ֵ���� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������2���� ![]() ��0��4����ȡһ������Ϊm���ٴ����µ��������У���ȡһ������Ϊn����k=mn��������������y=kx��ͼ����������һ���ĸ����� ��
��0��4����ȡһ������Ϊm���ٴ����µ��������У���ȡһ������Ϊn����k=mn��������������y=kx��ͼ����������һ���ĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����P�ڡ�AOB�ڣ���M��N�ֱ��ǵ�P����AO��BO����ֱ�ߵĶԳƵ㣮
��1������PEF���ܳ�Ϊ20����MN�ij���
��2������O=50�������EPF�Ķ�����
��3����ֱ��д����EPF���O��������ϵ��_____________________________

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com