
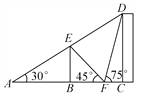
【题目】如图,楼房CD旁边有一池塘,池塘中有一电线杆BE高10米,在池塘边F处测得电线杆顶端E的仰角为45°,楼房顶点D的仰角为75°,又在池塘对面的A处,观测到A,E,D在同一直线上时,测得电线杆顶端E的仰角为30°.
(1)求池塘A,F两点之间的距离;
(2)求楼房CD的高.
【答案】(1)AF= (10![]() +10)米;(2)DC=(10+5
+10)米;(2)DC=(10+5![]() )米.
)米.
【解析】试题分析:(1)分别解Rt△ABE与Rt△BEF,可得AB与BF的大小.AF=AB+BF;
(2)设CD=x.在Rt△FCD中,可得CF的值,根据相似三角形的性质,可得比例关系求解.
试题解析:(1)在Rt△ABE中,
∵∠A=30°,BE=10,
∴![]()
∴AB=10![]()
在Rt△EBF中,
∵∠BFE=45°,
∴BF=BE=10,
∴AF=10+10![]() ;
;
(2)∵BE=10,∠A=30°,
∴AB=10![]() ,设CD=x,
,设CD=x,
设CD=x.则CF=![]() .
.
∵∠EBA=∠DCA=90°,∠A=30°,
∴△ABE∽△ACD,
由相似三角形的性质可得:![]() ,
,
即![]() ,
,
解得x=10+5![]() .
.
答:AF间的距离为(10+10![]() )米,楼房CD的高为(10+5
)米,楼房CD的高为(10+5![]() )米.
)米.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE是ΔABC的角平分线,AD是BC边上的高。若∠ABC=34°,∠ACB=64°,则∠DAE的大小是( )
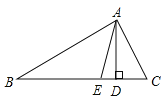
A. 5°B. 13°C. 15°D. 20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=![]() 的图象上,且sin∠BAC=
的图象上,且sin∠BAC=![]() .
.
(1)求k的值和边AC的长;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
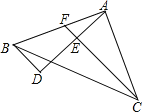
A. 6B. 5C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门).安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于第一、三象限内的
的图像交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,且四边形
,且四边形![]() 是平行四边形,点
是平行四边形,点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求该反比例函数和一次函数的表达式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com