
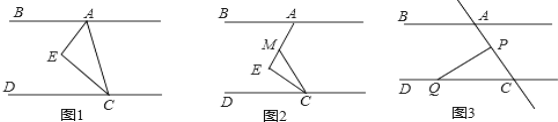
����Ŀ����ͼ1��CEƽ����ACD��AEƽ����BAC����EAC+��ACE=90��
��1�����ж�AB��CD��λ�ù�ϵ��˵�����ɣ�
��2����ͼ2������E=90�����ֲ��䣬�ƶ�ֱ�Ƕ���E��ʹ��MCE=��ECD����ֱ�Ƕ���E���ƶ�ʱ������BAE����MCD�Ƿ����ȷ����������ϵ����˵�����ɣ�
��3����ͼ3��PΪ�߶�AC��һ���㣬��QΪֱ��CD��һ���㣬������Q������CD���˶�ʱ����C���⣩��CPQ+��CQP����BAC�к�������ϵ��������۲�˵�����ɣ�������Q������CD�ķ����ӳ������˶�ʱ����C���⣩��CPQ+��CQP����BAC�к�������ϵ��ֱ��д��������ۣ�����˵�����ɣ�
���𰸡���1��AB��CD�����ɼ���������2����BAE+![]() ��MCD=90�������ɼ���������3������BAC=��PQC+��QPC ������PQC+��QPC+��BAC=180����
��MCD=90�������ɼ���������3������BAC=��PQC+��QPC ������PQC+��QPC+��BAC=180����
����������������1���ȸ���CEƽ�֡�ACD��AEƽ�֡�BAC�ó���BAC=2��EAC����ACD=2��ACE�����ɡ�EAC+��ACE=90���֪��BAC+��ACD=180�㣬�ʿɵó����ۣ���2����E��EF��AB������ƽ���ߵ����ʿ�֪EF��AB��CD����BAE=��AEF����FEC=��DCE���ʡ�BAE+��ECD=90�㣬���ɡ�MCE=��ECD���ɵó����ۣ���3������AB��CD��֪��BAC+��ACD=180�㣬��QPC+��PQC+��PCQ=180�㣬�ʡ�BAC=��PQC+��QPC������AB��CD�ó���BAC=��ACQ�����ɡ�PQC+��PCQ+��ACQ=180�㼴�ɵó����ۣ�
���������
��1����CEƽ�֡�ACD��AEƽ�֡�BAC��
���BAC=2��EAC����ACD=2��ACE��
�ߡ�EAC+��ACE=90�㣬 ���BAC+��ACD=180�㣬 ��AB��CD��
��2����BAE+![]() ��MCD=90�㣻
��MCD=90�㣻
 ��E��EF��AB��
��E��EF��AB��
��AB��CD��
��EF��AB��CD��
���BAE=��AEF����FEC=��DCE��
�ߡ�E=90�㣬 ���BAE+��ECD=90�㣬
�ߡ�MCE=��ECD��
���BAE+![]() ��MCD=90�㣻
��MCD=90�㣻
��3���١�BAC=��PQC+��QPC ���ڡ�PQC+��QPC+��BAC=180�㣮


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е�ʽ���β���ȷ���ǣ� ��
A.��x=y���õ�x+2=y+2
B.��2a��3=b��3���õ�2a=b
C.��m=n���õ�2am=2an
D.��am=an���õ�m=n
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��10��ѧ���������أ���50ǧ��Ϊ��������������Ϊ�������������Ϊ�����Ƶý������(��λ��ǧ��)��2, 3, ��7.5,��3, 5, ��8, 3.5, 4.5, 8, ��1.5
��10��ѧ����������Ϊ���٣�10��ѧ����ƽ������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������εIJ�ƺ����Ҫ�ڲ�ƺ�Ͻ�һ��ͤ�������Ϣ��Ҫʹ��ͤ����ƺ�����ߵľ�����ȣ���ͤ��λ��Ӧѡ�ڣ� ��
A.�����ε��������ߵĽ���
B.���������ߵĴ�ֱƽ���ߵĽ���
C.�����������ڽ�ƽ���ߵĽ���
D.����������������ֱ�ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����A��2��0����ֱ��l��y�ύ�ڵ�B��tan��OAB=![]() ��ֱ��l�ϵĵ�Pλ��y����࣬�ҵ�y��ľ���Ϊ1��
��ֱ��l�ϵĵ�Pλ��y����࣬�ҵ�y��ľ���Ϊ1��
��1����ֱ��l�ı���ʽ��
��2��������������![]() ��ͼ����P����m��ֵ��
��ͼ����P����m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ�㵽���ߵľ�����ȣ���������ǣ� ��
A.�����ߵĴ�ֱƽ���ߵĽ���B.�������ߵĽ���
C.������ƽ���ߵĽ���D.�����ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��Rt��ABC��б��BC�ϵ�һ�㣬��BD=AB����D��BC�Ĵ��ߣ���AC�ڵ�E����AE=5cm��DC=12 cm����CE�ij�Ϊ_____________ cm.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ�����������ߴ�ֱƽ���ߵĽ���λ�������εģ�������
A.��������B.��������C.б�ߵ��е�D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a2a3=a6
B.��x2��3=x6
C.m6��m2=m3
D.6a��4a=2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com