
【题目】如图,正方形ABCD的边长是4,点E是BC的中点,连接DE,DF⊥DE交BA的延长线于点F.连接EF、AC,DE、EF分别与C交于点P、Q,则PQ=_____.

【答案】![]()
【解析】
过点E作EM∥AB,交AC于点M,由题意可证ME∥AB∥CD,△ADF≌△CDE,可得AF=CE=ME,根据平行线分线段成比例可得![]() ,
,![]() ,
,![]() ,即可求PQ的长.
,即可求PQ的长.
如图,过点E作EM∥AB,交AC于点M,

∵四边形ABCD是正方形
∴AD=CD=BC=4,∠ADC=∠DAB=∠DCE=90°,∠ACE=45°,AB∥CD,
∴∠CDE+∠ADE=90°,AC=4![]()
∵DF⊥DE,
∴∠FDA+∠ADE=90°
∴∠CDE=∠FDA,且∠DAF=∠DCE=90°,AD=CD,
∴△ADF≌△CDE(AAS)
∴AF=CE,
∵点E是BC中点,
∴CE=BE=![]() BC=AF,
BC=AF,
∵ME∥CD
∴∠DCE=∠MEB=90°,且∠ACB=45°
∴∠CME=∠ACB=45°,
∴ME=CE=![]() BC,
BC,
∵ME∥AB,AB∥CD,
∴ME∥AB∥CD,
∴![]() ,
,![]() ,
,![]() ,
,
∴MQ=AQ,AM=CM=2![]() ,CP=2MP,
,CP=2MP,
∴MQ=![]() ,MP=
,MP=![]()
∴PQ=MQ+MP=![]()


科目:初中数学 来源: 题型:
【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED= °
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:

(1)用一种正多边形镶嵌平面
例如,用 6 个全等的正三角形镶嵌平面,摆放方案如图所示:
若用 m 个全等的正 n 边形镶嵌平面,求出 m,n 应满足的关系式;
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案;
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有 n 个,设这 n 个正多边形的边数分别为 x1,x2,…,xn,求出 x1,x2,…,xn 应满足的关系式.(用含 n 的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a0,a1,a2,a3,a4,…,满足下列条件:a0=0,a1=﹣|a0+1|,a2=﹣|a1+2|,a3=﹣|a2+3|,…,以此类推,a2019的值是( )
A. ﹣1009B. ﹣1010C. ﹣2018D. ﹣2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).

(1)求这两个函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.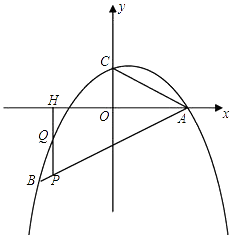
(1)试求此二次函数的解析式;
(2)试证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技进步,无人机的应用越来越广,如图,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部c的俯角.
(1)如果上述仰角与俯角分别为30。与60。 , 且该楼的高度为30米,求该时刻无人机的竖直高度CD.
(2)如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com