
【题目】如图1,点![]() 为线段
为线段![]() 上一点,一副直角三角板的直角顶点与点
上一点,一副直角三角板的直角顶点与点![]() 重合,直角边
重合,直角边![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .
.

(1)将图1中的三角板![]() 绕着点
绕着点![]() 沿顺时针方向旋转到如图2所示的位置,若
沿顺时针方向旋转到如图2所示的位置,若![]() ,则
,则![]() ________;猜想
________;猜想![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,三角板
的速度旋转一周,三角板![]() 不动,请问几秒时
不动,请问几秒时![]() 所在的直线平分
所在的直线平分![]() ?
?
(3)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,同时三角板
的速度旋转一周,同时三角板![]() 绕着点
绕着点![]() 沿顺时针方向按每秒
沿顺时针方向按每秒![]() 的速度旋转(随三角板
的速度旋转(随三角板![]() 停止而停止),请计算几秒时
停止而停止),请计算几秒时![]() 与
与![]() 的角分线共线.
的角分线共线.
【答案】(1)145°,180°;(2)3秒或15秒后OD所在的直线平分∠AOB;(3)![]() 秒或
秒或![]() 或
或![]() 秒后
秒后![]() 与
与![]() 的角分线共线.
的角分线共线.
【解析】
(1)根据互余关系先求出∠AOD,再由角的和差求出结果;
(2)当沿逆时针方向旋转45°或225°时,OD所在的直线平分∠AOB,由此便可求得结果;
(3)①当∠COD和∠AOB角平分线夹角为180时,②当∠COD和∠AOB角平分线重合时,即夹角为0°,③当∠COD和∠AOB角平分线重合后再次夹角为180°时,列出关于t的方程进行解答.
解:(1)∵∠COD=90°,∠AOC=35°,
∴∠AOD=∠COD-∠AOC=55°,
∵∠AOB=90°,
∴∠BOD=∠AOB+AOD=145°,
∵∠BOD=∠AOD+∠AOC+BOC,
∴∠AOC+∠BOD=∠AOC+∠AOD+∠AOC+∠BOC=∠COD+∠AOB=90°+90°=180°,
∴∠AOC+∠BOD=∠=180°,
故答案为:145°,180°;
(2)根据题意可得,
当旋转45°或225°时,OD所在的直线平分∠AOB,
所以,旋转时间为:45°÷15°=3(秒),225°÷15°=15(秒),
则3秒或15秒后OD所在的直线平分∠AOB;
(3)起始位置∠COD和∠AOB角平分线夹角为90°,
①当∠COD和∠AOB角平分线夹角为180时,
![]() ,
,
解得![]() (秒);
(秒);
②当∠COD和∠AOB角平分线重合时,即夹角为0°,
![]() ,
,
解得:![]() (秒);
(秒);
③当∠COD和∠AOB角平分线重合后再次夹角为180°时,
![]() ,
,
解得:![]() (秒);
(秒);
综上,![]() 秒或
秒或![]() 或
或![]() 秒后
秒后![]() 与
与![]() 的角分线共线.
的角分线共线.


科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
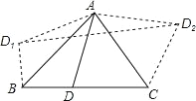
【题目】如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
+2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】白色污染( Whitepollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个)
年某个月丢弃塑料袋的数量(单位:个)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据上述数据,解答以下问题:

(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
分组 | 划记 | 频数 |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
合计 | / |
|
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,小彬又画出了如图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若该小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个的家庭个数.
个的家庭个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖为妈妈准备了一份生日礼物,礼物外包装盒为长方体形状,长、宽、高分别为![]() 、
、![]() 、
、![]()
![]() ,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为
,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为![]() ,
,![]() ,
,![]() (不计打结处丝带长度)
(不计打结处丝带长度)

(1)用含![]() 、
、![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() ,
,![]() ;
;
(2)方法简介:
要比较两数![]() 与
与![]() 大小,我们可以将
大小,我们可以将![]() 与
与![]() 作差,结果可能出现三种情况:
作差,结果可能出现三种情况:
①![]() ,则
,则![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() ,则
,则![]() ;
;
我们将这种比较大小的方法叫做“作差法”.
请帮小颖选出最节省丝带的打包方式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)当![]() 时,直接写出
时,直接写出![]() 的取值范围
的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5)B. (5,2)C. (2,﹣5)D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.
(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com