
分析 (1)利用解不等式的步骤与方法求得解集,进一步得出非负整数解;
(2)分别求得不等式的解集,进一步求得不等式组的解集即可;
(3)利用提取公因式法和平方差公式因式分解;
(4)整理代数式,进一步整体代入求得答案即可.
解答 (1)解:去分母:3x+3+2x-2≤6
移项:3x+2x≤6+2-3
合并同类项:5x≤5
系数化为1:x≤1
因此非负整数解为0,1;
(2)由①得:x≥1
由②得:x>2
在数轴上表示出来为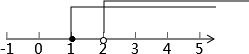
因此不等式组的解集为x>2;
(3)解:原式=m(x+y)(x-y);
(4)解:∵原式=2x(x-3y)+y(x-3y)+5
=(x-3y)(2x+y)+5
当2x+y=6,x-3y=1时
原式=1×6+5=11.
点评 此题考查解方程的步骤与方法,解不等式组与不等式以及整式的化简求值,掌握解答的步骤与方法是关键,注意整体思想的渗透.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
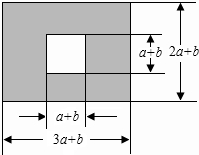 如图,学校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?(用a、b关系式表示)
如图,学校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?(用a、b关系式表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
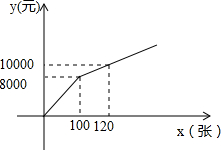 为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com