已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若一元二次方程mx2-(3m-1)x+2m-2=0的两个实数根分别为x1,x2.且|x1-x2|=2,求m的值.
【答案】
分析:(1)根据一元二次方程根的判别式,当△≥0时,方程有两个实数根,所以只需证明△≥0即可;
(2)利用一元二次方程根与系数的关系,首先将|x
1-x
2|=2,变形得出两根之和与两根之差的形式,结合x
1+x
2=-

,x
1x
2=
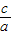
,求出即可.
解答:解:(1)①当m=0时,原方程为x-2=0,
解得:x=2,
所以方程有实数根;
②当m≠0时,
∵△=b
2-4ac
=[-(3m-1)]
2-4m(2m-2),
=(3m-1)
2-8m
2+8m,
=9m
2-6m+1-8m
2+8m,
=m
2+2m+1,
=(m+1)
2;
∴△=(m+1)
2≥0,
∴方程有实数根;
综上可知无论m取任何实数时,方程恒有实数根;
(2)∵一元二次方程mx
2-(3m-1)x+2m-2=0的两个实数根分别为x
1,x
2.
|x
1-x
2|=2,
∴x
1+x
2=-

=

,x
1x
2=

=

;
∴(x
1-x
2)
2=4,
∴x
12+x
22-2x
1x
2=4,
∴x
12+x
22+2x
1x
2-4x
1x
2=4,
∴(x
1+x
2)
2-4x
1x
2=4,
∴(

)
2-4×

=4,
∴整理得:-3m
2+2m-1=0,
解得:m
1=1,m
2=-

,
∴一元二次方程mx
2-(3m-1)x+2m-2=0的两个实数根分别为
x
1,x
2,且|x
1-x
2|=

,m的值为1或-

.
点评:此题主要考查了一元二次方程根与系数的关系,以及根的判别式,将|x
1-x
2|=2,正确的平方,得出两根之和与之差形式是解决问题的关键.

 ,x1x2=
,x1x2=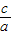 ,求出即可.
,求出即可. =
= ,x1x2=
,x1x2= =
= ;
; )2-4×
)2-4× =4,
=4, ,
, ,m的值为1或-
,m的值为1或- .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案