
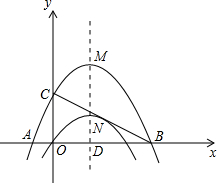
 已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.
已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.分析 (1)根据对称轴公式,待定系数法,可得函数关系式;
(2)根据正切函数,可得B点坐标,根据待定系数法,可得平移后的解析式,根据正切值,可得∠ABC=∠ACO,根据余角的性质,可得答案;
(3)根据线段CM与平移后的抛物线围成区域和线段ON与原抛物线围成的区域面积相等,可得以线段OC、MN和两抛物线所围成的区域的面积等于S四边形OCNM.
解答 解:(1)由图象经过原点,得
c=0,由对称轴等于3,得
x=-$\frac{b}{-2×\frac{1}{4}}$=3,解得b=$\frac{3}{2}$,
y=-$\frac{1}{4}$x2+$\frac{3}{2}$x;
(2)设平移后的抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+c,则OC=c,tan∠ABC=$\frac{1}{2}$,
∴OB=2c,则B点坐标为(2c,0),
把点B代入上式,得c=4,
∴平移后的抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4,
∵OA=2,OC=4,OB=8,tan∠ABC=tan∠ACO=$\frac{1}{2}$,
∴∠ABC=∠ACO,
∵OC⊥AB,
∴∠ABC+∠BCO=90°,
∴∠ACO+∠BCO=90°,
∴∠ACB=90°,
∴△ABC是直角三角形;
(3)如图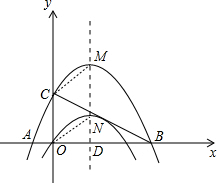 ,
,
连线CM,ON,由平移,得
OC平行且等于MN,
∴四边形OCNM是平行四边形,S四边形OCNM=OC•OD=12,
由平移,得
线段CM与平移后的抛物线围成区域和线段ON与原抛物线围成的区域面积相等,
则以线段OC、MN和两抛物线所围成的区域的面积等于S四边形OCNM=12.
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用正切函数的定义得出∠ABC=∠ACO,又利用了余角的性质;解(3)的关键是利用平移得出以线段OC、MN和两抛物线所围成的区域的面积等于S四边形OCNM.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄/岁 | 12 | 13 | 14 | 15 |
| 频数 | 6 | 9 | 15-a | a |
| A. | 平均数 | B. | 众数 | C. | 方差 | D. | 中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
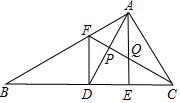 如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论
如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com