
【题目】计算:
(1)(﹣1)2 ![]()
(2)[(﹣3a)2+3ab2c]2ab2
(3)(﹣ ![]() )100×3101
)100×3101
(4)(2a+b)(b﹣2a)﹣(a﹣3b)2 .
【答案】
(1)解:原式=1+1+25=27
(2)解:原式=(9a2+3ab2c)2ab2=18a3b2+6a2b4c
(3)原式=(﹣ ![]() ×3)100×3=3
×3)100×3=3
(4)解:原式=b2﹣4a2﹣a2+6ab﹣9b2=﹣8b2﹣5a2+6ab
【解析】(1)原式利用乘方的意义,零指数幂、负整数指数幂法则计算即可得到结果;(2)原式利用单项式乘以多项式法则计算即可得到结果;(3)原式逆用积的乘方运算法则变形,计算即可得到结果;(4)原式利用平方差公式,以及完全平方公式化简,计算即可得到结果.
【考点精析】利用零指数幂法则和整数指数幂的运算性质对题目进行判断即可得到答案,需要熟知零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】已知,如图,AD⊥BC,EF⊥BC,∠BEF=∠ADG. 求证:DG∥AB.把证明的过程填写完整.
证明:因为AD⊥BC,EF⊥BC(已知),
所以∠EFB=∠ADB=90°()
所以EF∥()
所以∠BEF=()
因为∠BEF=∠ADG(已知)
所以()
所以DG∥AB()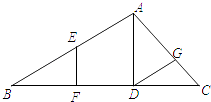
查看答案和解析>>
科目:初中数学 来源: 题型:
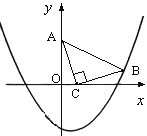
【题目】如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线![]() 上.
上.
(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
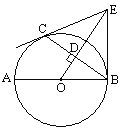
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.
(1)求证:BE与⊙O相切;
(2)连结AD并延长交BE于点F,若OB=6,且sin∠ABC=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个长方体的长为5.4×102 mm,宽为100 mm,高为2×102 mm,则此长方体的体积为( )
A. 1.08×105 mm3 B. 1.08×106 mm3 C. 1.08×107 mm3 D. 1.08×108 mm3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com