
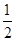 时,
时,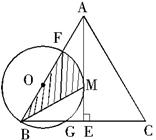
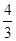 ;
; .
.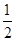 得到∠C=60°,则可判断△ABC为等边三角形,所以AB=AC=BC=4,则∠OAM=30°,根据含30度的直角三角形三边的关系得到AO=2R,则2R+R=4,解得R=
得到∠C=60°,则可判断△ABC为等边三角形,所以AB=AC=BC=4,则∠OAM=30°,根据含30度的直角三角形三边的关系得到AO=2R,则2R+R=4,解得R=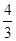 ;
;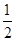 OB=
OB=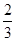 ,BH=
,BH=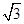 OH=
OH=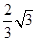 ,所以BM=
,所以BM=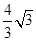 ,然后根据扇形面积公式和三角形面积公式和S阴=S扇形FOM+S△OBM进行计算.
,然后根据扇形面积公式和三角形面积公式和S阴=S扇形FOM+S△OBM进行计算.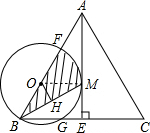
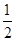 ,
,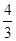 ,
,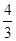 ;
;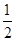 OB=
OB=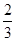 ,BH=
,BH=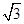 OH=
OH=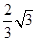 ,
,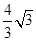 ,
,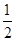 OH•BM=
OH•BM=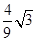 ,
,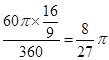
 .
.

科目:初中数学 来源:不详 题型:解答题
| 名称 | 四等分圆的面积 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
| 选用的工具 | 带刻度的三角板 | 量角器 | 带刻度的三角板、圆规 |
| 画出示意图 | 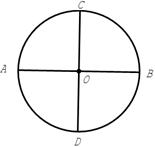 | | |
| 简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. | | |
| 指出对称性 | 既是轴对称图形又是中心对称图形 | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.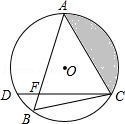
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
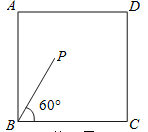
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
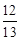 ,cos 67.4°=
,cos 67.4°=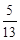 ,tan 67.4° =
,tan 67.4° =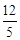 )
)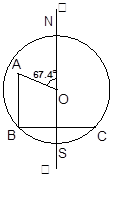
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com