
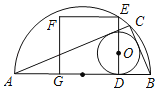
【题目】如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆上.
(1)当正方形的顶点F也在半圆弧上时,半圆的半径与正方形边长的比为 ;
(2)当正方形DEFG的面积为100,且△ABC的内切圆⊙O的半径r=4,求半圆的直径AB的值;
(3)若半圆的半径为R,直接写出⊙O半径r可取得的最大值.
【答案】(1)![]() ;(2)AB=21;(3)
;(2)AB=21;(3)![]()
【解析】
(1)根据圆和正方形的对称性可知:![]() ,在直角三角形FGH中,利用勾股定理可得
,在直角三角形FGH中,利用勾股定理可得![]() ,从而用含a的代数式表示半圆的半径为
,从而用含a的代数式表示半圆的半径为![]() ,正方形边长为2a,所以可求得半圆的半径与正方形边长的比;
,正方形边长为2a,所以可求得半圆的半径与正方形边长的比;
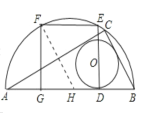
(2)切点分别为I,J,连接EB、AE,OJ、OI,可得OJCI是正方形,且边长是4,可设BD=x,AD=y,则BD=BJ=x,AD=AI=y,分别利用直角三角形ABC和直角三角形AEB中的勾股定理和相似比作为相等关系列方程组求解即可求得半圆的直径AB=21.
(3)根据(2)中得出方程解答即可.
解:(1)如图,根据圆和正方形的对称性可知:![]() ,
,
H为半圆的圆心,
不妨设GH=a,则GF=2a,
在直角三角形FGH中,由勾股定理可得![]() ,由此可得,半圆的半径为
,由此可得,半圆的半径为![]() ,正方形边长为2a,
,正方形边长为2a,
所以半圆的半径与正方形边长的比是![]() ;
;
(2)因为正方形DEFG的面积为100,所以正方形DEFG边长为10.
切点分别为I,J,连接EB、AE,OI、OJ,
∵AC、BC是⊙O的切线,
∴CJ=CI,∠OJC=∠OIC=90°,
∵∠ACB=90°,
∴四边形OICJ是正方形,且边长是4,
设BD=x,AD=y,则BD=BI=x,AD=AJ=y,
在直角三角形ABC中,由勾股定理得(x+4)2+(y+4)2=(x+y)2①;
在直角三角形AEB中,
∵∠AEB=90°,ED⊥AB,
∴△ADE∽△BDE∽△ABE,
∴![]() 即ED2=ADBD,即102=xy②.
即ED2=ADBD,即102=xy②.
解①式和②式,得x+y=21,
即半圆的直径AB=21;
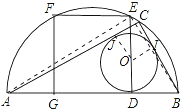
(3)由(2)可得:![]() ,
,
当点C与点E重合且为半圆弧的中点时,⊙O半径r可取得的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+2经过点A(m,-2),将点A向右平移7个单位长度,得到点B,抛物线![]() 的顶点为C.
的顶点为C.
(1)求m的值和点B的坐标;
(2)求点C的坐标(用含n的代数式表示);
(3)若抛物线与线段AB只有一个公共点,结合函数图象,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年五月,我国南方某省A、B两市遭受严重洪涝灾害,邻近县市C、D决定调运物资支援A、B两市灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市,A市需要的物资比B市需要的物资少100吨.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)A、B两市各需救灾物资多少吨?
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计如表所示:
自选项目 | 人数 | 频率 |
立定跳远 | b | 0.18 |
三级蛙跳 | 12 | 0.24 |
一分钟跳绳 | 8 | a |
投掷实心球 | 16 | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若该校九年级共有400名学生,试估计年级选择“一分钟跳绳”项目的总人数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
科目:初中数学 来源: 题型:
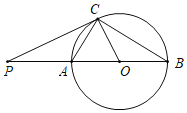
【题目】如图,已知AB是⊙O的直径,AC是弦,点P是BA延长线上一点,连接PC、BC,∠PCA=∠B.
(1)求证:PC是⊙O的切线;
(2)若PC=4,PA=2,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
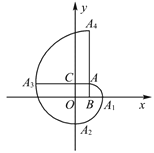
【题目】如图,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 的坐标为
的坐标为![]() ,弧
,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,继续以点
为半径的圆弧,继续以点![]() 为圆心,按上述作法得到的曲线
为圆心,按上述作法得到的曲线![]() …,称为正方形的“渐开线”,则点
…,称为正方形的“渐开线”,则点![]() 的坐标是______.
的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
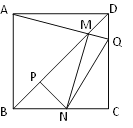
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com