
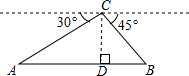
 马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号)
马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号) 分析 图中两个直角三角形中,都是知道已知角和对边,根据正切函数求出邻边后,相加求和即可.
解答 解:由已知,得∠A=30°,∠B=45°,CD=400米,
∵CD⊥AB于点D.
∴在Rt△ACD中,∠CDA=90°,tanA=$\frac{CD}{AD}$,
∴AD=$\frac{CD}{tanA}$=$\frac{400}{\frac{\sqrt{3}}{3}}$=400$\sqrt{3}$,
在Rt△BCD中,∠CDB=90°,∠B=45°
∴DB=CD=400米,
∴AB=AD+DB=400$\sqrt{3}$+400=400($\sqrt{3}$+1)米.
故答案为400($\sqrt{3}$+1).
点评 本题考查了解直角三角形的应用,解决本题的关键是利用CD为直角△ABC斜边上的高,将三角形分成两个三角形,然后求解.分别在两三角形中求出AD与BD的长.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
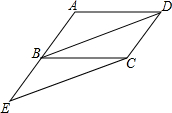 已知:如图,在?ABCD中,延长AB到E,使得BE=AB,连接BD、CE.
已知:如图,在?ABCD中,延长AB到E,使得BE=AB,连接BD、CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com