
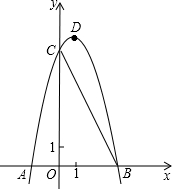
 如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(-2,0),B两点,与y轴交于C点,tan∠ABC=2.
如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(-2,0),B两点,与y轴交于C点,tan∠ABC=2.分析 (1)由OC=8、tan∠ABC=2得点B坐标,将点A、B坐标代入求解可得;
(2)先求出直线CD解析式和点E、F坐标,设平移后解析式为y=-(x-1)2+9+m,结合图象根据抛物线与线段EF(含线段端点)只有1个公共点,求得临界时m的值,从而得出答案,
解答 解:(1)由抛物线的表达式知,点C(0,8),即 OC=8;
Rt△OBC中,OB=OC•tan∠ABC=8×$\frac{1}{2}$=4,
则点B(4,0).
将A、B的坐标代入抛物线的表达式中,
得:$\left\{\begin{array}{l}{4a-2b+8=0}\\{16a+4b+8=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴抛物线的表达式为y=-x2+2x+8,
∵y=-x2+2x+8=-(x-1)2+9,
∴抛物线的顶点坐标为D(1,9).
(2)设直线CD的表达式为y=kx+8,
∵点D(1,9),
∴直线CD表达式为y=x+8.
∵过点A、B作x轴的垂线,交直线CD于点E、F,
可得:E(-2,6),F(4,12).
设抛物线向上平移m个单位长度(m>0),
则抛物线的表达式为:y=-(x-1)2+9+m;
当抛物线过E(-2,6)时,m=6,
当抛物线过F(4,12)时,m=12,
∵抛物线与线段EF(含线段端点)只有1个公共点,
∴m的取值范围是6<m≤12.
点评 本题主要考查待定系数法求函数解析式及抛物线与直线的交点问题,利用图象与线段只有一个交点得出临界是m的值是解题关键


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
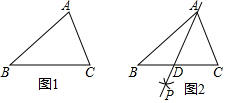 下面是“作三角形一边中线”的尺规作图过程.
下面是“作三角形一边中线”的尺规作图过程.查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
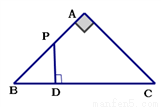
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. 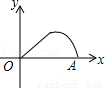 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
将一副三角板如图放置,使点在上,则∠AFE的度数为( )

A. 45° B. 50° C. 60° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
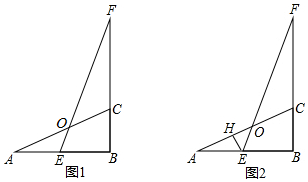
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com