
 已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).
已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).分析 (1)首先求出A、B两点坐标,利用待定系数法即可解决问题.
(2)利用描点法画出函数图象即可.
(3)根据图象二次函数的图象在一次函数的图象上方,即可写出自变量的取值范围.
解答 解:(1)∵二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5),
∴m-1+1=0,n=1=5,即n=4,
∴点A(-1,0),点B(4,5),
∴$\left\{\begin{array}{l}{1-b+c=0}\\{16+4b+c=5}\end{array}\right.$解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴二次函数的吉祥物为y=x2-2x-3.
(2)这两个函数图象如图所示,
(3)由图象可知,x2+bx+c>x+1时,x<-1或x>4.
点评 本题考查二次函数的应用、一次函数的应用、待定系数法等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会利用图象根据条件确定自变量的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
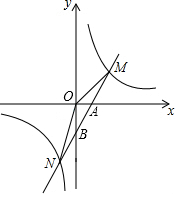 如图所示,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(-2,-8),一次函数y=ax+b与x轴交于点A,与y轴交于点B.
如图所示,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(-2,-8),一次函数y=ax+b与x轴交于点A,与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
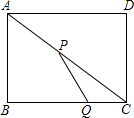 如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1个单位/秒的速度从点C出发,沿CB向点B移动,当P、Q两点中其中一点到达终点时停止运动,在P、Q两点移动过程中,当△PQC为等腰三角形时,求时间t的值.
如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1个单位/秒的速度从点C出发,沿CB向点B移动,当P、Q两点中其中一点到达终点时停止运动,在P、Q两点移动过程中,当△PQC为等腰三角形时,求时间t的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
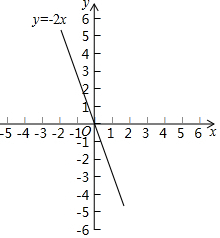 已知正比例函数y1=-2x的图象如图.
已知正比例函数y1=-2x的图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
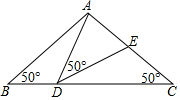 如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
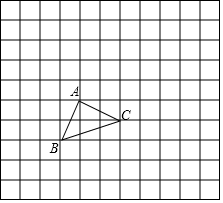 如图,△ABC在方格纸中
如图,△ABC在方格纸中查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某人在山坡坡脚A处测得电视塔BC塔尖B的仰角为60°,沿山坡AM走到D处测得塔尖B的仰角为30°,已知AC为100米,山坡坡度i=1:3,C、A、E三点在同一直线上.求此人所在位置点D的铅直高度DE.(结果保留根号形式)
如图,某人在山坡坡脚A处测得电视塔BC塔尖B的仰角为60°,沿山坡AM走到D处测得塔尖B的仰角为30°,已知AC为100米,山坡坡度i=1:3,C、A、E三点在同一直线上.求此人所在位置点D的铅直高度DE.(结果保留根号形式)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com