
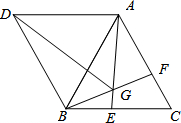
 如图,平行四边形ADBC中,∠C=60°,AC=BC,点E、F分别在BC、AC上,BE=CF,AE=BF交于点G.
如图,平行四边形ADBC中,∠C=60°,AC=BC,点E、F分别在BC、AC上,BE=CF,AE=BF交于点G.分析 (1)根据三角形全等的判定方法可证得△ABE≌△BCF,则∠BAE=∠FBC,利用三角形外角性质得∠BGE=∠ABG+∠BAE,即可得到结论;
(2)延长GE至点H,使GH=GB,由于∠BGE=60°,根据等边三角形的判定得到△BGH为等边三角形,然后根据等边三角形的性质得到BG=BH=GH,∠GBH=60°,且AB=BD,∠ABD=60°,易得∠ABH=∠DBG,根据三角形全等的判定方法可证得△DBG≌△ABH(SAS),则DG=AH,即可得到DG=AG+BG.
解答 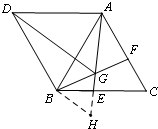 (1)解:∠C=60°,AC=BC,
(1)解:∠C=60°,AC=BC,
∴△ABC是等边三角形,
∴∠ABC=∠C=60°,
∵在△ABE和△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠C}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠FBC,
∴∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°;
(2)证明:延长GE至点H,使GH=GB,如图,
∵∠BGE=60°,
∴△BGH为等边三角形,
∴BG=BH=GH,∠GBH=60°,
∵四边形ADBC是平行四边形,
∴△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∵∠ABH=∠GBH+∠ABG,∠DBG=∠ABD+∠ABG,
∴∠ABH=∠DBG,
∵在△DBG和△ABH中,
$\left\{\begin{array}{l}{DB=AB}\\{∠DBG=∠ABH}\\{BG=BH}\end{array}\right.$,
∴△DBG≌△ABH(SAS),
∴DG=AH,
而AH=AG+GH,
∴DG=AG+BG.
点评 本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等边三角形的判定与性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
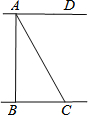 如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.| A. | $\frac{45}{cos50°}$ | B. | 45•cos50° | C. | $\frac{45}{tan50°}$ | D. | 45•tan50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 8065 | B. | 8064 | C. | 8063 | D. | 8062 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明在做数学练习时,遇到下面的题目:
小明在做数学练习时,遇到下面的题目:
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
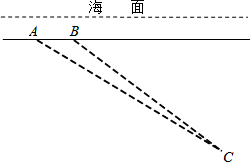 如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为2000m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)
如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为2000m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com