
 如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.
如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP. 分析 作AD⊥BC于D,则∠ADB=∠ADP=90°,由勾股定理得AB2=AD2+BD2,AP2=AD2-DP2,得出AB2-AP2=BD2-DP2=(BD+DP)(BD-DP),再由等腰三角形的性质得出BD=CD,即可得出结论.
解答 证明:作AD⊥BC于D,如图所示:
则∠ADB=∠ADP=90°,
∴AB2=AD2+BD2,AP2=AD2-DP2,
∴AB2-AP2=BD2-DP2=(BD+DP)(BD-DP)=BP(BD-DP),
∵AB=AC,AD⊥BC,
∴BD=CD,
∴AB2-AP2=BP(BD-DP)=BP(CD-DP)=BP•CP.
点评 本题考查了勾股定理、等腰三角形的性质、平方差公式;熟练掌握等腰三角形的性质,运用勾股定理和平方差公式进行计算是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆的面积S和半径R之间的关系 | |
| B. | 匀速行驶的汽车,行驶的路程s与时间t之间的关系 | |
| C. | 一个正数的平方根与它本身之间的关系 | |
| D. | 电阻一定,加在这个电阻两端的电压通过这个电阻的电流之间的关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
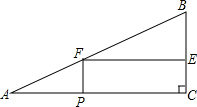 如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD
如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com