
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��BC��![]() ��ֱ��BD��x�ύ�ڵ�A����B��2��3������D��0��
��ֱ��BD��x�ύ�ڵ�A����B��2��3������D��0��![]() ����
����
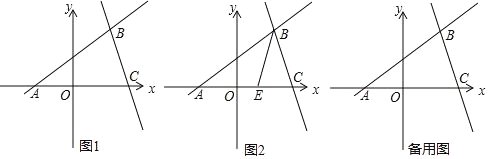
��1����ֱ��BD�ĺ�������ʽ��
��2����y������һ��P��ʹ�á�ABC���ACP�������ȣ������P�����ꣻ
��3����ͼ2��EΪ�߶�AC��һ�㣬����BE��һ����F�ӵ�B���������߶�BE��ÿ��1����λ�˶�����E�����߶�EA��ÿ��![]() ����λ�˶���A��ֹͣ�����F�������˶�����������ʱ��Ϊt����t����Сֵ��
����λ�˶���A��ֹͣ�����F�������˶�����������ʱ��Ϊt����t����Сֵ��
���𰸡���1��y=![]() x+
x+![]() ����2��P��0��3����0��-3������3��
����2��P��0��3����0��-3������3��![]()
��������
��1����ֱ��BD�Ľ���ʽy=kx+b����B��2��3����D��0��![]() ��������룬���ô���ϵ�����������
��������룬���ô���ϵ�����������
��2��������ABC����ACP�������ȣ��ó�P��������ľ���ֵ���ٸ��ݵ�P��y���ϣ��Ӷ�ȷ����P������
��3����������ɵ�![]() ������A����б��Ϊ45�ȵ�ֱ��l2������E��EF��l2���ڵ�F����B��E��F���㹲���Ҵ�ֱ��ֱ��l2ʱ��t��С����t=BF���������ֱ��l2��ֱ��BF�Ľ��㣬�Ӷ����F�������꣬�̶����BF�����ɣ�
������A����б��Ϊ45�ȵ�ֱ��l2������E��EF��l2���ڵ�F����B��E��F���㹲���Ҵ�ֱ��ֱ��l2ʱ��t��С����t=BF���������ֱ��l2��ֱ��BF�Ľ��㣬�Ӷ����F�������꣬�̶����BF�����ɣ�
�⣺��1����ֱ��BD�Ľ���ʽΪ��y=kx+b��
�� B��2��3����D��0��![]() ������������ʽ
������������ʽ
�ã� ��ã�
��ã�![]()
��ֱ��BD�ı���ʽΪ��y=![]() x+
x+![]() ��
��
��2������ABC����ACP��������
����ABC����ACPͬ�ף�
��![]()
�ߵ�P��y���ϣ�
��![]()
��P��0��3����0��-3��
��3����������ɵã�![]()
����A����б��Ϊ45�ȵ�ֱ��l2������E��EF��l2���ڵ�F��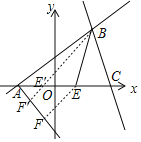
��EF=![]() AE����t=BE+EF��
AE����t=BE+EF��
��B��E��F���㹲���Ҵ�ֱ��ֱ��l2ʱ��t��С������t=![]() ����
����
ֱ��l2�ı���ʽΪ��y=-x-2��ֱ��BF����ʽΪ��y=x+1��
��������������ʽ��������ã�![]() ������F��
������F��![]()
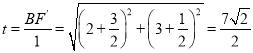 s
s



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֤��ȫ�������εĶ�Ӧ��ƽ������ȡ�
��1�������ʺ������ͼ�Σ������ͼ��д����֪����֤��
��2������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() ��
��![]() ��Ҫ����
��Ҫ����![]() ��
��![]() ���صľ��룬�ס��ҡ�����������ͬѧ�ֱ�����˲����߶εij��ȺͽǵĶ������õ������������ݣ��ף�
���صľ��룬�ס��ҡ�����������ͬѧ�ֱ�����˲����߶εij��ȺͽǵĶ������õ������������ݣ��ף�![]() ��
��![]() ���ң�
���ң�![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �����������
�����������![]() ��
��![]() ���ؾ�����У� ��
���ؾ�����У� ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ3cm�ĵȱ������Σ���P��Q�ֱ�Ӷ���A��Bͬʱ���������߶�AB��BC�˶��������ǵ��ٶȶ�Ϊ1cm/s.����P�����Bʱ��P��Q����ֹͣ�˶�.���P���˶�ʱ��Ϊt��s����
��1����tΪ��ֵʱ����PBQ��ֱ�������Σ�
��2������AQ��CP���ཻ�ڵ�M�����P��Q���˶��Ĺ����У���CMQ��仯�����仯,��˵�����ɣ������䣬��������Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ����ij��������·����֧���y(Ʊ���������ȥ��Ӫ�ɱ�)��˿���x�ĺ���ͼ��.Ŀǰ������·����Ϊ��Ť�����йز��ž��������Ʊ�۵���֤��.�˿ʹ�����Ϊ��������˾Ӧ��Լ��Դ�����ƹ�����������Ӫ�ɱ����Դ˾�ʵ��Ť��.������˾��Ϊ����Ӫ�ɱ������½�����˾�����������Ʊ�۲���Ť��.�������������������ͼ�ٷֱ�Ļ���ͼ�ں�ͼ�ۣ�����˵����ȷ���ǣ� ��
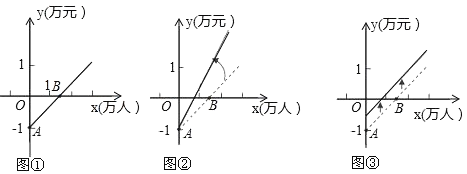
A.��A��ʾ���ǹ�������˾Ʊ��Ϊ1ԪB.��B��ʾ�˿�Ϊ0��
C.��Ӧ�˿�������Ǣ�D.��Ӧ������˾������Ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=nx2��3nx��4n��n��0����x�ύ��B��C���㣨��B�ڵ�C����ࣩ������������y�ύ�ڵ�A��
��1����B�������� ������C�������� ����
��2������BAC=90�����������ߵĽ���ʽ��
��3����M�ǣ�2�����������ϵĶ��㣬��N����Գ����ϵĶ��㣬�Ƿ���������ĵ�M��N��ʹ����A��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ADΪ��ABC�����ߣ��ӳ�AD��E��ʹDE��AD��
��1����֤������ACD�ա�EBD��
��2����������������������⣺��ͼ2��ADΪ��ABC�����ߣ�BMI��AD��C����AC��M����AM��GM����֤��BG��AC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��������
��������![]() �Ŀ��ڴ�С�����ڷ�����ȫ��ͬ���Ҷ�����ֱ��
�Ŀ��ڴ�С�����ڷ�����ȫ��ͬ���Ҷ�����ֱ��![]() �ϣ����㵽
�ϣ����㵽![]() ��ľ���Ϊ
��ľ���Ϊ![]() ����������ߵĽ���ʽΪ________��
����������ߵĽ���ʽΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣���֪��MAN=135����������ABCD�Ƶ�A��ת��
��1����������ABCD��ת����MAN���ⲿ������A���⣩ʱ��AM��AN�ֱ���������ABCD�ı�CB��CD���ӳ��߽��ڵ�M��N������MN��
����ͼ1����BM=DN�����߶�MN��BM+DN֮���������ϵ�� ��
����ͼ2����BM��DN�����ж����е�������ϵ�Ƿ��Գ������������������֤����������������˵�����ɣ�
��2����ͼ3����������ABCD��ת����MAN���ڲ�������A���⣩ʱ��AM��AN�ֱ���ֱ��BD���ڵ�M��N��̽�������߶�BM��MN��DN�ij���Ϊ���߳����������Ǻ��������Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com