
【题目】在平面直角坐标系xOy中,O为原点,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.过点P作PB∥x轴,与直线AQ交于点B,如果AP⊥BO,求点P的坐标.
科目:初中数学 来源: 题型:
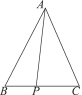
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)(1)如图①,点E、F、G、H分别在平行四边形ABCD的边AB、BC、CD、DA上,连结EF、FG、GH、HE,将△AEH、△BFE、△CGF、△DHG分别沿EF、FG、GH、HE折叠,折叠后的图形恰好能拼成一个无重叠、无缝隙的矩形.若![]() ,
,![]() ,求
,求![]() 的长.
的长.
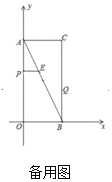
(拓展)(2)参考图②,四边形ABCD是平行四边形,![]() ,当按图①的方式折叠后的图形能拼成一个无重叠、无缝隙的正方形时,则
,当按图①的方式折叠后的图形能拼成一个无重叠、无缝隙的正方形时,则![]() ___________.
___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
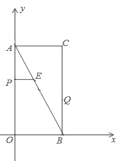
【题目】如图,在平面直角坐标系中,已知矩形![]() 的顶点
的顶点![]() 的坐标是
的坐标是![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动.点
运动.点![]() 、
、![]() 的运动速度均为每秒1个单位,过点
的运动速度均为每秒1个单位,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,一点到达,另一点即停.设点
,一点到达,另一点即停.设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() .
.
(1)填空:用含![]() 的代数式表示下列各式
的代数式表示下列各式
![]() __________,
__________,![]() __________.
__________.
(2)①当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离.
的距离.
②当点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() 时,直接写出
时,直接写出![]() 的值.
的值.
(3)在动点![]() 、
、![]() 运动的过程中,点
运动的过程中,点![]() 是矩形
是矩形![]() (包括边界)内一点,且以
(包括边界)内一点,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,直接写出点
为顶点的四边形是菱形,直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
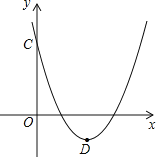
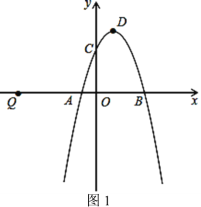
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌的饮水机接通电源后就进入自动程序:开机加热到水温 100℃, 停止加热,水温开始下降,此时水温 y(℃)与开机后用时 x(min)成反比 例关系,直至水温降至 30℃,饮水机关机.饮水机关机后即刻自动开机,重 复上述自动程序.若在水温为 30℃时,接通电源后,水温 y(℃)和时间 x(min)的关系如图所示,水温从 100℃降到 35℃所用的时间是________min.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=-x2+2x+3的图象与x轴交于点A、B,与y轴交于点C,顶点为D.
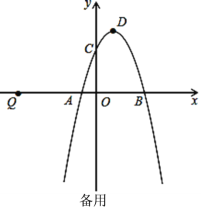
(1)写出A、B、D三点的坐标;
(2)若P(0,t)(t<-1)是y轴上一点,Q(-5,0),将点Q绕着点P顺时针方向旋转90°得到点E.当点E恰好在该二次函数的图象上时,求t的值;
(3)在(2)的条件下,连接AD、AE.若M是该二次函数图象上一点,且∠DAE=∠MCB,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)﹣(3)题
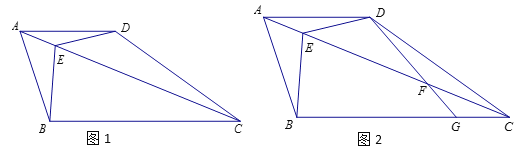
数学课上,老师出示了这样一道题:如图,四边形ABCD,AD∥BC,AB=AD,E为对角线AC上一点,∠BEC=∠BAD=2∠DEC,探究AB与BC的数量关系.
某学习小组的同学经过思考,交流了自己的想法:
小柏:“通过观察和度量,发现∠ACB=∠ABE”;
小源:“通过观察和度量,AE和BE存在一定的数量关系”;
小亮:“通过构造三角形全等,再经过进一步推理,就可以得到线段AB与BC的数量关系”.
……
老师:“保留原题条件,如图2, AC上存在点F,使DF=CF=![]() AE,连接DF并延长交BC于点G,求
AE,连接DF并延长交BC于点G,求![]() 的值”.
的值”.
(1)求证:∠ACB=∠ABE;
(2)探究线段AB与BC的数量关系,并证明;
(3)若DF=CF=![]() AE,求
AE,求![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将与2022年2月20日在北京举行,北京将成为历史上第一座举办过夏奥会又举办过冬奥会的城市,东宝区举办了一次冬奥会知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
(收集数据)
从甲、乙两校各随机抽取20名学生,在这次竞赛中它们的成绩如下:
甲 | 30 | 60 | 60 | 70 | 60 | 80 | 30 | 90 | 100 | 60 |
60 | 100 | 80 | 60 | 70 | 60 | 60 | 90 | 60 | 60 | |
乙 | 80 | 90 | 40 | 60 | 80 | 80 | 90 | 40 | 80 | 50 |
80 | 70 | 70 | 70 | 70 | 60 | 80 | 50 | 80 | 80 |
(整理、描述数据)按如下分数段整理、描述这两组样本数据:
(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)
学校 | 平均分 | 中位数 | 众数 |
甲 | 67 | 60 | 60 |
乙 | 70 | 75 | a |
30≤x≤50 | 50<x≤80 | 80<x≤100 | |
甲 | 2 | 14 | 4 |
乙 | 4 | 14 | 2 |
(分析数据)两组样本数据的平均分、中位数、众数如右表所示:其中a= .
(得出结论)
(1)小伟同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是 校的学生;(填“甲”或“乙”)
(2)老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为 ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com