
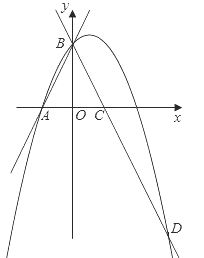
ЁОЬтФПЁПШчЭМЃЌжБЯпy=2x+2гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌАбЁїAOBбиyжсЗелЃЌЕуAТфЕНЕуCЃЌЙ§ЕуBЕФХзЮяЯпy=-x2+bx+cгыжБЯпBCНЛгкЕуDЃЈ3ЃЌ-4ЃЉЃЎ
ЃЈ1ЃЉЧѓжБЯпBDКЭХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЕквЛЯѓЯоФкЕФХзЮяЯпЩЯЃЌЪЧЗёДцдквЛЕуMЃЌзїMNДЙжБгкxжсЃЌДЙзуЮЊЕуNЃЌЪЙЕУвдMЁЂOЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїBOCЯрЫЦЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкжБЯпBDЩЯЗНЕФХзЮяЯпЩЯгавЛЖЏЕуPЃЌЙ§ЕуPзїPHДЙжБгкxжсЃЌНЛжБЯпBDгкЕуHЃЌЕБЫФБпаЮBOHPЪЧЦНааЫФБпаЮЪБЃЌЪдЧѓЖЏЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉжБЯпBDЕФНтЮіЪНЮЊЃКy=-2x+2ЃЛy=-x2+x+2ЃЛЃЈ2ЃЉЃЈ1ЃЌ2ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЛђЃЈ2ЃЌ0ЃЉЃЎ
ЃЉЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЛђЃЈ2ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩжБЯпy=2x+2ПЩвдЧѓГіAЃЌBЕФзјБъЃЌгЩД§ЖЈЯЕЪ§ЗЈОЭПЩвдЧѓГіХзЮяЯпЕФНтЮіЪНКЭжБЯпBDЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌ2ЃЌгЩЃЈ1ЃЉЕФНтЮіЪНЩшMЃЈaЃЌ-a2+a+2ЃЉЃЌЕБЁїBOCЁзЁїMONЛђЁїBOCЁзЁїONMЪБЃЌгЩЯрЫЦШ§НЧаЮЕФаджЪОЭПЩвдЧѓГіНсТлЃЛ
ЃЈ3ЃЉЩшPЃЈbЃЌ-b2+b+2ЃЉЃЌHЃЈbЃЌ-2b+2ЃЉЃЎгЩЦНааЫФБпаЮЕФаджЪНЈСЂЗНГЬЧѓГіbЕФжЕОЭПЩвдЧѓГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпy=2x+2ЃЌ
ЁрЕБx=0ЪБЃЌy=2ЃЌ
ЁрBЃЈ0ЃЌ2ЃЉЃЎ
ЕБy=0ЪБЃЌx=-1ЃЌ
ЁрAЃЈ-1ЃЌ0ЃЉЃЎ
ЁпХзЮяЯпy=-x2+bx+cЙ§ЕуBЃЈ0ЃЌ2ЃЉЃЌDЃЈ3ЃЌ-4ЃЉЃЌ
Ёр![]()
НтЕУЃК![]() ЃЌ
ЃЌ
Ёрy=-x2+x+2ЃЛ
ЩшжБЯпBDЕФНтЮіЪНЮЊy=kx+bЃЌгЩЬтвтЃЌЕУ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпBDЕФНтЮіЪНЮЊЃКy=-2x+2ЃЛ
ЃЈ2ЃЉДцдкЃЎ
ШчЭМ1ЃЌ
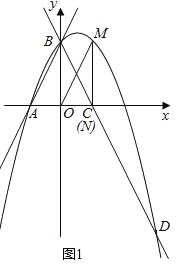
ЩшMЃЈaЃЌ-a2+a+2ЃЉЃЎ
ЁпMNДЙжБгкxжсЃЌ
ЁрMN=-a2+a+2ЃЌON=aЃЎ
Ёпy=-2x+2ЃЌ
Ёрy=0ЪБЃЌx=1ЃЌ
ЁрCЃЈ1ЃЌ0ЃЉЃЌ
ЁрOC=1ЃЎ
ЁпBЃЈ0ЃЌ2ЃЉЃЌ
ЁрOB=2ЃЎ
ЕБЁїBOCЁзЁїMNOЪБЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃКa1=1ЃЌa2=-2ЃЈЩсШЅЃЉ
ЁрMЃЈ1ЃЌ2ЃЉЃЛ
ШчЭМ2ЃЌ
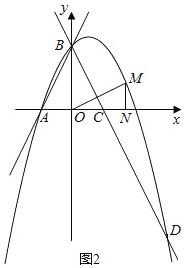
ЕБЁїBOCЁзЁїONMЪБЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрa=![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁрЗћКЯЬѕМўЕФЕуMЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЩшPЃЈbЃЌ-b2+b+2ЃЉЃЌHЃЈbЃЌ-2b+2ЃЉЃЎ
ШчЭМ3ЃЌ
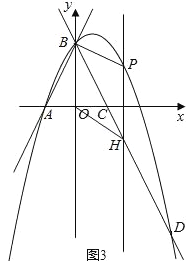
ЁпЫФБпаЮBOHPЪЧЦНааЫФБпаЮЃЌ
ЁрBO=PH=2ЃЎ
ЁпPH=-b2+b+2+2b-2=-b2+3bЃЎ
Ёр2=-b2+3b
Ёрb1=1ЃЌb2=2ЃЎ
ЕБb=1ЪБЃЌPЃЈ1ЃЌ2ЃЉЃЌ
ЕБb=2ЪБЃЌPЃЈ2ЃЌ0ЃЉ
ЁрPЕуЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЛђЃЈ2ЃЌ0ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЕШбќШ§НЧаЮЕФСНБпГЄЗжБ№ЪЧ aКЭ 2aЃЋ1ЃЈaЃО0ЃЉЃЌдђЫќЕФжмГЄЮЊЃЈ ЃЉ
A. 3aЃЋ1B. 4aЃЋ1C. 5aЃЋ2D. 4aЃЋ1 Лђ 5aЃЋ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСааджЪжаЃЌСтаЮОпгаЖјОиаЮВЛвЛЖЈОпгаЕФЪЧЃЈ ЃЉ.
A. ЖдНЧЯпЯрЕШЃЛB. ЖдНЧЯпЛЅЯрЦНЗжЃЛ
C. ЖдНЧЯпЛЅЯрДЙжБЃЛD. ЖдНЧЯрЕШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЕу A 2, 1 ЯђзѓЦНвЦ 3 ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ 4 ИіЕЅЮЛГЄЖШЕУЕНЕу B ЃЌдђЕу B ЕФзјБъЪЧЃЈ ЃЉ
A. 5, 3B. 1, 3C. 1, 5D. 5, 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2+2x+mЉ1=0гаСНИіЪЕЪ§ИљЃЌдђmЕФШЁжЕЗЖЮЇЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћ3x3mЉ2Љ2y2+n+10=0ЪЧЖўдЊвЛДЮЗНГЬЃЌФЧУДmn=ЁЁ __________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП5ИіКьЧђЁЂ4ИіАзЧђЗХШывЛИіВЛЭИУїЕФКазгРяЃЌДгжаУўГі6ИіЧђЃЌЧЁКУКьЧђгыАзЧђЖМУўЕНЃЌетМўЪТЧщЪєЃЈ ЃЉ
A. ВЛПЩФмЗЂЩњ B. ПЩФмЗЂЩњ C. КмПЩФмЗЂЩњ D. БиШЛЗЂЩњ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕуDЮЊЁїABCБпBCЕФбгГЄЯпЩЯвЛЕуЃЎ
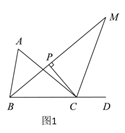
ЃЈ1ЃЉШєЁЯAЁУЁЯABC=3ЁУ4ЃЌЁЯACD=140ЁуЃЌЧѓЁЯAЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЁЯABCЕФНЧЦНЗжЯпгыЁЯACDЕФНЧЦНЗжЯпНЛгкЕуMЃЌЙ§ЕуCзїCPЁЭBMгкЕуPЃЎ
ЧѓжЄЃК ![]() ЃЛ
ЃЛ
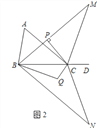
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЁїMBCвджБЯпBCЮЊЖдГЦжсЗелЕУЕНЁїNBCЃЌЁЯNBCЕФНЧЦНЗжЯпгыЁЯNCBЕФНЧЦНЗжЯпНЛгкЕуQЃЈШчЭМ2ЃЉЃЌЪдЬНОПЁЯBQCгыЁЯAгадѕбљЕФЪ§СПЙиЯЕЃЌЧыаДГіФуЕФВТЯыВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЉІaЉІ= 8ЃЌЉІbЉІ= 2.
ЃЈ1ЃЉЕБaЁЂbЭЌКХЪБЃЌЧѓa+bЕФжЕЃЛ
ЃЈ2ЃЉЕБaЁЂbвьКХЪБЃЌЧѓa+bЕФжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com