
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.

(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.
解:(1)∵抛物线与直线y2=x+1的一个交点的横坐标为2,
∴交点的纵坐标为2+1=3,即交点坐标为(2,3)。
设抛物线的解析式为y1=a(x﹣1)2+4,把交点坐标(2,3)代入得:
3=a(2﹣1)2+4,解得a=﹣1。
∴抛物线解析式为:y1=﹣(x﹣1)2+4=﹣x2+2x+3。.
(2)令y1=0,即﹣x2+2x+3=0,解得x1=3,x2=﹣1,
∴抛物线与x轴交点坐标为(3,0)和(﹣1,0)。
在坐标系中画出抛物线与直线的图形,如图:
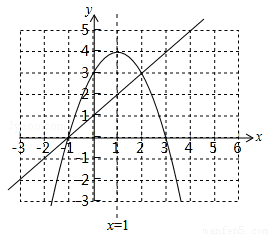
根据图象,可知使得y1≥y2的x的取值范围为﹣1≤x≤2。
(3)由(2)可知,点A坐标为(3,0)。
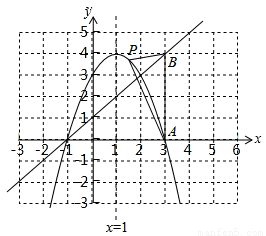
令x=3,则y2=x+1=3+1=4,
∴B(3,4),即AB=4。
设△PAB中,AB边上的高为h,
则h=|xP﹣xA|=|xP﹣3|。
∴S△PAB=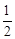 AB•h=
AB•h=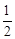 ×4×|xP﹣3|=2|xP﹣3|.
×4×|xP﹣3|=2|xP﹣3|.
∵S△PAB≤6,∴2|xP﹣3|≤6,化简得:|xP﹣3|≤3。
去掉绝对值符号,将不等式化为不等式组:
﹣3≤xP﹣3≤3,解此不等式组,得:0≤xP≤6。
∴当S△PAB≤6时,点P的横坐标x的取值范围为0≤xP≤6。
【解析】
试题分析:(1)首先求出抛物线与直线的交点坐标,然后利用待定系数法求出抛物线的解析式。
(2)确定出抛物线与x轴的两个交点坐标,依题意画出函数的图象.由图象可以直观地看出使得y1≥y2的x的取值范围。
(3)首先求出点B的坐标及线段AB的长度;设△PAB中,AB边上的高为h,则由S△PAB≤6可以求出h的范围,这是一个不等式,解不等式求出xP的取值范围。


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
 ,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?查看答案和解析>>
科目:初中数学 来源: 题型:044
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设A(x1,y1)、B(x2,y2)是抛物线与直线的两个交点,点P是线段AB的中点,且点P的横坐标为![]() ,试用含a的代数式表示点P的纵坐标;
,试用含a的代数式表示点P的纵坐标;
(3)设A,B两点的距离d=![]() ·|x1-x2|,试用含a的代数式表示d.
·|x1-x2|,试用含a的代数式表示d.
查看答案和解析>>
科目:初中数学 来源:2008年江西省中考数学试卷(解析版) 题型:解答题
 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com