
分析 (1)由题意$\left\{\begin{array}{l}{-\frac{b}{2a}=-\frac{3}{2}}\\{16a-4b=2}\\{c=0}\end{array}\right.$,解方程组即可解决问题;
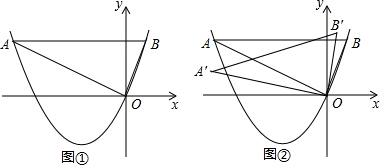
(2)存在.如图1中,作BD∥AO交x轴于D.易知四边形ABDO是平行四边形,此时△BOD≌△OBA,推出OD=AB=5,由此即可解决问题;
(3)如图2中,当OA′与x轴负半轴重合时,A′B′交OA于E,证明此时OE是△A′OB′的中线,△A′OB′的重心在中线OA上,求出中线A′B′的解析式即可解决问题,当OA′与x轴的正半轴重合时,同法可得点P的坐标;
解答 解:(1)由题意$\left\{\begin{array}{l}{-\frac{b}{2a}=-\frac{3}{2}}\\{16a-4b=2}\\{c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{3}{2}}\\{c=0}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{2}$x2+$\frac{3}{2}x$.
当y=2时,$\frac{1}{2}$x2+$\frac{3}{2}x$=0,解得x=1或-4,
∵A(-4,2),
∴B(1,2),
令y=0,$\frac{1}{2}$x2+$\frac{3}{2}x$=0解得x=-3或0,
∴抛物线与x轴的另一个交点坐标为(-3,0);
(2)存在.理由如下:
如图1中,作BD∥AO交x轴于D.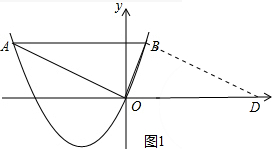
∵AB∥OD,AO∥BD,
∴四边形ABDO是平行四边形,
∴AB=OD,OA=BD,∵OB=BO,
∴△BOD≌△OBA,
∴OD=AB=5,
∴D(5,0);
(3)如图2中,当OA′与x轴负半轴重合时,A′B′交OA于E,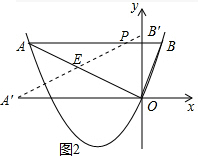
∴∠A=∠B′A′O=∠AOA′,
∴EA′=EO,
∵∠B′A′O+∠A′B′O=90°,∠A′OE+∠EOB′=90°,
∴∠EOB′=∠EB′O,
∴EO=EB′,
∴EA′=EB′,
∴OE是△A′OB′的中线,此时△A′OB′的重心在中线OA上,
易知A′(-2$\sqrt{5}$,0),B′(0,$\sqrt{5}$),
∴中线A′B′的解析式为y=$\frac{1}{2}$x+$\sqrt{5}$,
当y=2时,2=$\frac{1}{2}$x+$\sqrt{5}$,
∴x=4-2$\sqrt{5}$,
∴P(4-2$\sqrt{5}$,2).
当OA′与x轴的正半轴重合时,同法可得点P的坐标为(4+2$\sqrt{5}$,2),
综上所述,满足条件的点P坐标为(4-2$\sqrt{5}$,2)或(4+2$\sqrt{5}$,2);
点评 本题考查二次函数综合题、一次函数的应用、全等三角形的判定和性质、平行四边形的判定和性质、三角形重心的定义等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,学会寻找特殊位置解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
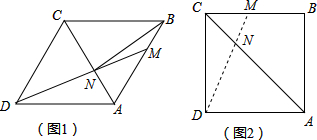
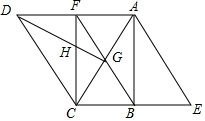 如图,在Rt△ABC中,∠ABC=90°,∠ACB=60°,将Rt△ABC绕点C逆时针旋转60°得到△DGC,点G在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABE,连接AD.
如图,在Rt△ABC中,∠ABC=90°,∠ACB=60°,将Rt△ABC绕点C逆时针旋转60°得到△DGC,点G在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABE,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
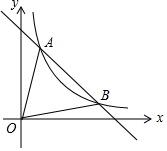 如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
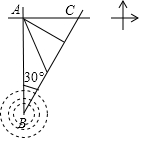 台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.
台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com