
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 如图1,作辅助线,构建三角形的高线,根据∠B=45°得△BDC是等腰直角三角形,求出BD和CD的长,利用勾股定理求出AD的长,计算∠A的正弦值,对③作出判断;
利用计算AE的长,从而计算BE的长,与BC比较可以得出∠C为钝角,对①作出判断;
如图2,根据同弧所对的圆心角是圆周角的2倍得:△AOC是等腰直角三角形,根据斜边AC=5,可计算半径OA的长,对②作出判断;
如图3,利用正六边形的特殊性质得:△OEF是等边三角形,从而根据半径OA的长,计算DF的长,得出边长EF,对④作出判断.
解答 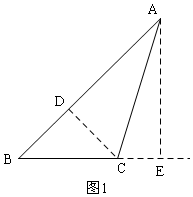 解:如图1,过C作CD⊥AB于D,过A作AE⊥BC于E,
解:如图1,过C作CD⊥AB于D,过A作AE⊥BC于E,
∵∠B=45°,
∴△BDC是等腰直角三角形,
∵BC=3$\sqrt{2}$,
∴BD=CD=3,
由勾股定理得:AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴sin∠BAC=$\frac{CD}{AC}$=$\frac{3}{5}$,
所以③正确;
由S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$CB•AE,
∴7×3=3$\sqrt{2}$AE,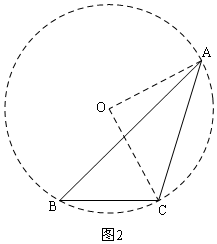
AE=$\frac{7}{\sqrt{2}}$=$\frac{7\sqrt{2}}{2}$,
在Rt△ABE中,
BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{{7}^{2}-(\frac{7\sqrt{2}}{2})^{2}}$=$\sqrt{\frac{49}{2}}$>BC=3$\sqrt{2}$=$\sqrt{18}$,
∴∠ACB>90°,
即∠C一定是钝角;
所以①正确;
如图2,设△ABC的外接圆的圆心为O,连接OA、OC,
∵∠B=45°,
∴∠AOC=2∠B=90°,
∵OA=OC,
∴△AOC是等腰直角三角形,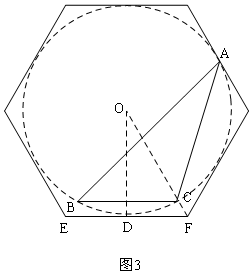
∵AC=5,
∴OA=$\frac{5}{\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$,
则△ABC的外接圆半径为$\frac{5\sqrt{2}}{2}$;
所以②不正确;
如图3,此正六边形是△ABC的外接圆的外切正六边形,
Rt△ODF中,由②得:OD=$\frac{5\sqrt{2}}{2}$,
由题意得:△OEF是等边三角形,
∴∠OFE=60°,
tan60°=$\frac{OD}{DF}$=$\frac{\frac{5\sqrt{2}}{2}}{DF}$,
∴DF=$\frac{5\sqrt{2}}{2}$×$\frac{1}{\sqrt{3}}$=$\frac{5\sqrt{6}}{6}$,
∴EF=2DF=$\frac{5\sqrt{6}}{3}$,
则△ABC外接圆的外切正六边形的边长是$\frac{5\sqrt{6}}{3}$,
所以④正确,
故本题正确的结论有:①③④;3个;
故选C.
点评 本题考查了等边三角形、正六边形、外接圆、内切圆等知识点,解题的关键是正确地利用正六边形中相等的元素和圆的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
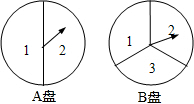 小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.
小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m+n)(-m-n)=m2-n2 | B. | (2a-b)2=4a2-2ab+b2 | ||
| C. | (x+3)(-x+3)=x2-9 | D. | (4x+1)2=16x2+8x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
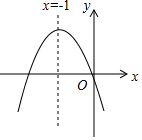 已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=-1,且经过原点.下列结论:(1)b2-4ac>0;(2)a-b+c>0;(3)abc>0(4)b=2a,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=-1,且经过原点.下列结论:(1)b2-4ac>0;(2)a-b+c>0;(3)abc>0(4)b=2a,其中正确的有( )| A. | .1个 | B. | .2个 | C. | .3个 | D. | .4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=20米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=20米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )| A. | 90米 | B. | 98米 | C. | 80米 | D. | 88米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com