
【题目】如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.

(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
【答案】(1)y=-x2-2x+3,顶点C的坐标为(-1,4);(2)证明见解析.
【解析】
(1)解:∵y=x+3与坐标轴分别交与A,B两点,∴A点坐标(-3,0)、B点坐标(0,3).
∵抛物线y=ax2+bx-3a经过A,B两点,
∴![]()
解得![]()
∴抛物线解析式为:y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C的坐标为(-1,4).
(2)证明:∵B,D关于MN对称,C(-1,4),B(0,3),
∴D(-2,3).∵B(0,3),A(-3,0),∴OA=OB.
又∠AOB=90°,∴∠ABO=∠BAO=45°.
∵B,D关于MN对称,∴BD⊥MN.
又∵MN⊥x轴,∴BD∥x轴.
∴∠DBA=∠BAO=45°.
∴∠DBO=∠DBA+∠ABO=45°+45°=90°.
设直线BC的解析式为y=kx+b,
把B(0,3),C(-1,4)代入得,
![]() 解得
解得![]()
∴y=-x+3.
当y=0时,-x+3=0,x=3,∴E(3,0).
∴OB=OE,又∵∠BOE=90°,
∴∠OEB=∠OBE=∠BAO=45°.
∴∠ABE=180°-∠BAE-∠BEA=90°.
∴∠ABC=180°-∠ABE=90°.
∴∠CBD=∠ABC-∠ABD=45°.
∵CM⊥BD,∴∠MCB=45°.
∵B,D关于MN对称,
∴∠CDM=∠CBD=45°,CD∥AB.
又∵AD与BC不平行,∴四边形ABCD是梯形.
∵∠ABC=90°,∴四边形ABCD是直角梯形.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,请你按照下面要求完成尺规作图.
,请你按照下面要求完成尺规作图.
①以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ,
,
②再分别以![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,
,
③连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
请你判断以下结论:
①![]() 是
是![]() 的一条角平分线;②连接
的一条角平分线;②连接![]() ,
,![]() 是等边三角形;③
是等边三角形;③![]() ;
;
④点![]() 在线段
在线段![]() 的垂直平分线上;⑤
的垂直平分线上;⑤![]() .其中正确的结论有________(只需要写序号).
.其中正确的结论有________(只需要写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图(1)若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A′B′C′D′相似吗?请说明理由;
(2)如图(2),x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
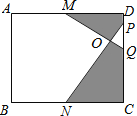
【题目】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=![]() DC.若AB=16,BC=20,则图中阴影部分的面积是 .
DC.若AB=16,BC=20,则图中阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具![]() 小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米
小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米![]() 分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程
分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程![]() 米
米![]() 与时间
与时间![]() 分钟
分钟![]() 的关系如图,请结合图象,解答下列问题:
的关系如图,请结合图象,解答下列问题:

![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 若小军的速度是120米
若小军的速度是120米![]() 分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
![]() 在
在![]() 的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com