
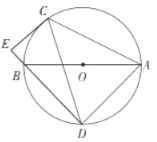
【题目】如图,AB为⊙O的直径,C、D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E.
(1)连接AC、AD,求证:∠DAC+∠ACE=180°.
(2)若∠ABD=2∠BDC,求证:CE是⊙O的切线.
【答案】(1)见解析(2)见解析
【解析】
(1)根据圆周角定理证得∠ADB=90°,即AD⊥BD,由CE⊥DB证得AD∥CE,根据平行线的性质即可证得结论;
(2)连接OC.先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC∥DB,再由CE⊥DB,得到OC⊥CE,根据切线的判定即可证明CE为⊙O的切线.
(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥DB,
∵CE⊥DB,
∴AD∥CE,
∴∠DAC+∠ACE=180°;
(2)连接OC.如图:
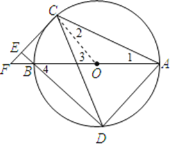
∵OA=OC,
∴∠1=∠2.
又∵∠3=∠1+∠2,
∴∠3=2∠1.
又∵∠4=2∠BDC,∠BDC=∠1,
∴∠4=2∠1,
∴∠4=∠3,
∴OC∥DB.
∵CE⊥DB,
∴OC⊥CE.
又∵OC为⊙O的半径,
∴CE为⊙O的切线;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于点F,交AD的延长线于点E,若AB=4,BM=2,则△DEF的面积为( )

A.9B.8C.15D.14.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)若BC=4,求AG的长;
(2)连接BF,求证:AB=FB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=x的图象与反比例函数y=![]() (k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(Ⅰ)当x=4时,求反比例函数y=![]() 的值;
的值;
(Ⅱ)当﹣2<x<﹣1时,求反比例函数y=![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
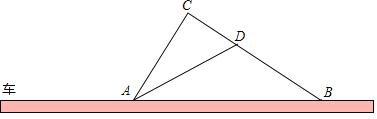
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com