
【题目】如图,平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 、
、![]() 分别是对角线BD上的两点,给出下列四个条件:①
分别是对角线BD上的两点,给出下列四个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中能判断四边形
.其中能判断四边形![]() 是平行四边形的个数是
是平行四边形的个数是

A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据平行四边形的判定及全等三角形的性质即可作出判断.
解:A、∵在平行四边形ABCD中,OA=OC,OB=OD,
若BE=DF,则OE=OF,
∴四边形AECF是平行四边形;
B、∵在平行四边形ABCD中,OA=OC,OB=OD,
若DE=BF,则OE=OF,
∴四边形AECF是平行四边形;
C、若∠BAE=∠DAF,不能判断四边形![]() 是平行四边形;
是平行四边形;
D、∵在平行四边形ABCD中,AD∥BC,AD=BC
∴∠ADB =∠DBC ,
∵∠BCE=∠DAF,
在△DAF和△BCE中,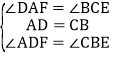 ,
,
∴△DAF≌△BCE,
∴ DF=BE,
∵在平行四边形ABCD中,OA=OC,OB=OD,
∴OE=OF,
∴四边形AECF是平行四边形.
故选:C.


科目:初中数学 来源: 题型:
【题目】已知:∠AOB=90°,∠COD=20°,OM平分∠AOC,ON平分∠BOD.
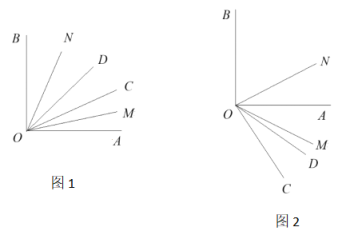
(1)如图1,∠COD在∠AOB内部,且∠AOC=30°.则∠MON的大小为 .
(2)如图1,∠COD在∠AOB内部,若∠AOC的度数未知,是否能求出∠MON的大小,若能,写出你的解答过程;若不能,说明理由.
(3)如图2,∠COD在∠AOB外部(OM在OD上方,∠BOC![]() 180°),试求出∠MON的大小.
180°),试求出∠MON的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
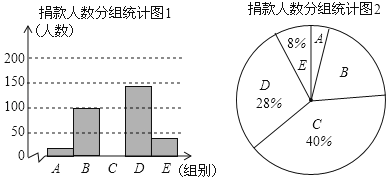
【题目】昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5.
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | 40≤x<50 |
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a,b,定义两种新运算“※”与“◎”,规定: a※b=a2+2ab,a◎b=|a+ b|-|a- b|,例如,2※(- 1)=22+2×2×(-1)=0,(- 2) ※3=|-2+3|-| - 2-3|= -4.![]() b c
b c
(1)计算(- 3) ※2的值;
(2)若a, b在数轴上的位置如图所示,化简a◎b;
![]()
(3)若(-2) ※x=2◎(- 4)+ 3x,求x的值:
(4)对于任意有理数m,n,请你定义一种新运算“★” ,使得(-3) ★5 = 4,直接写出你定义的运算:m★n=_ (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
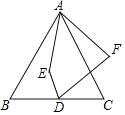
【题目】如图,等边△ABC中,AB=10,D为BC的中点,E为△ABC内一动点,DE=3,连接AE,将线段AE绕点A逆时针旋转60°得AF,连接DF,求线段DF的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com