
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�ƣ����۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����y=��10x+500�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�60%��
��1����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��2�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������ÿ�µ���������Ƕ��٣�
��3�����С����Ҫÿ�»�õ�������2000Ԫ����ôС��ÿ�µijɱ�������Ҫ����Ԫ�����ɱ�=��������������
���𰸡���1![]() ��20��x��32������2�������۵��۶�Ϊ32Ԫʱ��ÿ�¿ɻ������������������2160Ԫ����3��3600��
��20��x��32������2�������۵��۶�Ϊ32Ԫʱ��ÿ�¿ɻ������������������2160Ԫ����3��3600��
�������������������1��������ã�ÿ�������������۵���֮��Ĺ�ϵ�ɽ��ƿ���һ�κ���������=�����������ۣ������������Ӷ��г���ϵʽ��
��2������ȷ�����κ����ĶԳ��ᣬȻ�������������ȷ��������ɣ�
��3�����������ߵ����ʺ�ͼ�����ÿ�µijɱ���
�����������1�������⣬�ã�w=��x��20��y=��x��20������10x+500��=![]() ����
����![]() ��20��x��32����
��20��x��32����
��2�����ں���![]() ��ͼ��ĶԳ�����ֱ��x=
��ͼ��ĶԳ�����ֱ��x=![]() =35��
=35��
����a=��10��0�������߿������£�����20��x��32ʱ��W����X���������������x=32ʱ��W=2160
�𣺵����۵��۶�Ϊ32Ԫʱ��ÿ�¿ɻ������������������2160Ԫ��
��3��ȡW=2000�ã�![]()
��������̵ã� ![]() =30��
=30�� ![]() =40��
=40��
��a=��10��0�������߿������£�����30��x��40ʱ��w��2000��
��20��x��32������30��x��32ʱ��w��2000��
��ÿ�µijɱ�ΪP��Ԫ���������⣬�ã�P=20����10x+500��=��200x+10000
��k=��200��0����P��x���������С������x=32ʱ��P��ֵ��С��P��Сֵ=3600��
����Ҫÿ�»�õ�������2000Ԫ��С��ÿ�µijɱ�����Ϊ3600Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ������
�ס�������ͬʱ�����25ǧ��A��ȥB �������ﳵ�Ҳ��������ٶ����ҵ��ٶȵ�3��������B��ͣ��40������Ȼ���B�ط���A������;������������ʱ�����dz�����ʱ��ǡ��3Сʱ�������˵��ٶȸ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx+b��k��0����˫����y=![]() �ཻ�ڵ�A��m��6���͵�B����3��n����ֱ��AB��y�ύ�ڵ�C��
�ཻ�ڵ�A��m��6���͵�B����3��n����ֱ��AB��y�ύ�ڵ�C��
��1����ֱ��AB�ı���ʽ��
��2����AC��CB��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��90������BOC��30����OMƽ�֡�AOC��ONƽ�֡�BOC��

��1�����MON�Ķ�����
��2������BOC��60���������������䣬���MON���� ����
��3������AOB�����������������䣬���MON�Ķ�����
��4��������Ľ���ܿ���ʲô���ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������������ɸ��ⳤΪ3cm��С�������ɵģ������桢���濴���ļ��������״ͼ��ͼ��ʾ��
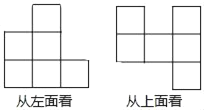
��1���ü������������� ����С��������ɣ�������� ����С��������ɣ�
��2�����ü��������״�̶��ã�
����ü�������������ֵ��
����Ҫ�������Сʱ�ļ��������Ϳ�����ᣬ����Ϳ�����������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ǻ�����ʶ����ǿ��Խ��Խ�����ѡ���̼���У�����Ʒ�Ƶ�ɽ�����г����Ͷ���г�.˳�糵�����·�![]() �ͳ�������������Ϊ
�ͳ�������������Ϊ![]() Ԫ��
Ԫ��![]() �ͳ�������������Ϊ
�ͳ�������������Ϊ![]() Ԫ.��
Ԫ.��![]() �ͳ�������������
�ͳ�������������![]() �ͳ���
�ͳ���![]() ������֪����
������֪����![]() �ͳ���
�ͳ���![]() �ͳ�ÿ���ɶ����
�ͳ�ÿ���ɶ����![]() Ԫ.
Ԫ.
��1����ÿ��![]() �ͳ���
�ͳ���![]() �ͳ�����������
�ͳ�����������
��2�����ó��мƻ�һ�ι���![]() �����ͺŵ����г���
�����ͺŵ����г���![]() ̨��ȫ���۳�������
̨��ȫ���۳�������![]() �ͳ��Ľ�������������
�ͳ��Ľ�������������![]() �ͳ���
�ͳ���![]() ������ó��й���
������ó��й���![]() �ͳ���
�ͳ���![]() �ͳ���������������ʹ���������������������������Ƕ��٣�
�ͳ���������������ʹ���������������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̽������̴����������д���������Ͷ���߹������̺����ɿ����̴�����5�꣬5���������ɿ������Ա�ԭ���̱�۸�20%�ļ۸���лع���Ͷ���߿����������ֹ��̷���������ѡ��
����һ���������̱��һ���Ը����̿ÿ��ɻ�õ����Ϊ���̱�۵�10%��
�������������̱�۵İ���һ���Ը����̿ǰ3�����̵��������鿪�������У�3���ÿ��ɻ�õ����Ϊ���̱�۵�9%
��1����Ͷ����ѡ�����ֹ��̷�����5�������õ�Ͷ�������ʸ��ߣ�Ϊʲô��
��ע��Ͷ��������=![]() ��100%��
��100%��
��2����ͬһ��۵����̣���ѡ���˹��̷���һ����ѡ���˹��̷���������ô5������˻�õ��������7.2��Ԫ���ʼ������˸�Ͷ���˶�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB=�� ����PD=�� ����
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ɸ���ȫ��ͬ��С��������ɵ�һ�������壮
��1��������ʵ��������������˳�λ�����������������ͼ������ͼ����ͼ��

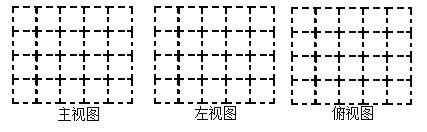
��2�������������������õ�һЩС�����壬��������������������ͼ����ͼ���䣬��ô�������õ�___________С�����壻
��3������������������������һЩ��ͬ��С�����壬��������������������ͼ����ͼ���䣬��ô������������________��С�����壮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com