
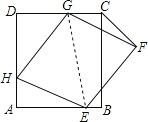
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.

【答案】详见解析
【解析】
试题分析:(1)连接GE,根据正方形的性质和平行线的性质得到∠AEG=∠CGE,根据菱形的性质和平行线的性质得到∠HEG=∠FGE,解答即可;
(2)证明Rt△HAE≌Rt△GDH,得到∠AHE=∠DGH,证明∠GHE=90°,根据正方形的判定定理证明.
证明:(1)连接GE,
∵AB∥CD,
∴∠AEG=∠CGE,
∵GF∥HE,
∴∠HEG=∠FGE,
∴∠HEA=∠CGF;
(2)∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HAE和Rt△GDH中,
![]() ,
,
∴Rt△HAE≌Rt△GDH(HL),
∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴菱形EFGH为正方形;


科目:初中数学 来源: 题型:
【题目】阅读材料:
分解因式:x2+2x-3
解:原式=x2+2x+1-1-3
=(x2+2x+1)-4
=(x+1)2-4
=(x+1+2)(x+1-2)
=(x+3)(x-1)
此种方法抓住了二次项和一次项的特点,然后加一项,使这三项成为完全平方式,我们把这种分解因式的方法叫配方法.请仔细体会配方法的特点,然后尝试用配方法解决下列问题:
(1)分解因式:m2-4mn+3n2;
(2)无论m取何值,代数式m2-3m+2015总有一个最小值,请你尝试用配方法求出它的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据相关报道,截止到今年四月,我国已完成5.78万个农村教学点的建设任务.5.78万可用科学记数法表示为( )
A.5.78×103
B.57.8×103
C.0.578×104
D.5.78×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织初一、初二学生举行“四城同创”宣传活动,从学校坐车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度保持不变,在A地仍要宣传8分钟,则他们从B地返回学校用的时间是( )
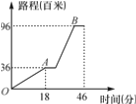
A. 48分钟 B. 45.2分钟 C. 46分钟 D. 33分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com