
【题目】某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水的价格x(元)的一次函数.
(1)根据下表提供的数据,求y与x的函数关系式;当水价为每吨10元时,1吨水生产出的饮料所获的利润是多少?
1吨水价格x(元) | 4 | 6 |
用1吨水生产的饮料所获利润y(元) | 200 | 198 |
(2)为节约用水,这个市规定:该厂日用水量不超过20吨时,水价为每吨4元;日用水量超过20吨时,超过部分按每吨40元收费.已知该厂日用水量不少于20吨,设该厂日用水量为t吨,当日所获利润为W元,求W与t的函数关系式;该厂加强管理,积极节水,使日用水量不超过25吨,但仍不少于20吨,求该厂的日利润的取值范围.
【答案】(1)y=-x+204;194元;(2)4000≤W≤4820.
【解析】
(1)用1吨水生产的饮料所获利润y(元)是1吨水的价格x(元)的一次函数.可以设出一次函数关系式,然后根据表中所给的条件(4,200)(6,198)可求出解析式;
(2)根据函数式可求出一吨水价是40的利润,然后根据题意可得w=200×20+164(t-20),代入t=20或t=25可求出日利润的取值范围.
(1)设y关于x的一次函数式为:![]() 根据题意得:
根据题意得:
![]()
解得![]()
∴所求一次函数式是y=x+204,
当x=10时,y=10+204=194(元);
(2)当1吨水的价格为40元时,所获利润是:y=40+204=164(元).
∴W与t的函数关系式是w=200×20+(t20)×164,
即w=164t+720,
∵ 20 ≤ t ≤ 25,
∴ 4000≤W≤4820.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,tan∠C= ![]() ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系. 
时段 | x | 还车数 | 借车数 | 存量y |
6:00﹣7:00 | 1 | 45 | 5 | 100 |
7:00﹣8:00 | 2 | 43 | 11 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= , 解释m的实际意义:;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:O0这个时段的还车数比借车数的3倍少4,求此时段的借车数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣8交y轴于点A,交x轴正半轴于点B.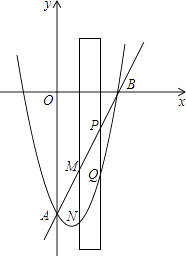
(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于y轴,在点A、B之间平行移动,直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ,设M点的横坐标为m,且0<m<3.试比较线段MN与PQ的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com