Question

5．已知菱形OABC在坐标系中的位置如图所示，O是坐标原点，点C（1，2），点A在x轴上．点M（0，2）．

（1）点P是直线OB 上的动点，求PM+PC最小值．
（2）将直线y=-x-1向上平移，得到直线y=kx+b．
①当直线y=kx+b与线段OC有公共点时，结合图象，直接写出b的取值范围．
②当直线y=kx+b将四边形OABC分成面积相等的两部分时，求k，b．

Answer 1

分析 （1）连接AC、AM，由四边形OABC是菱形，可得出PC=PA，根据三角形两边之和大于第三边即可得出PC+PM的取值范围，再利用勾股定理求出AM即可得出结论；
（2）根据平移的性质找出k值．①画出图形，分别代入O（0，0）、C（1，2）即可求出b的取值范围；
②连接AC、OB，设AC与OB的交点为D，当直线y=-x+b过点D时，直线y=-x+b将四边形OABC分成面积相等的两部分，根据点A、C的坐标求出点D的坐标，利用待定系数法求出b值即可得出结论．

解答 解：（1）由已知，OA=OC=$\sqrt{{2^2}+{1^2}}=\sqrt{5}$，连接AC、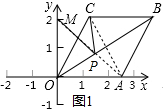AM，如图1所示．
∵四边形OABC是菱形，
∴PC=PA，
∴PC+PM=PM+PA≤AM，
即PC+PM≤$\sqrt{O{M}^{2}+O{A}^{2}}$=$\sqrt{{2}^{2}+（\sqrt{5}）^{2}}$=3．
（2）∵y=kx+b为y=-x-1平移得来的，
∴k=-1．
①依照题意画出图形，如图2所示．

结合函数图象可知，当点O在直线y=-x+b上时，b最小，此时b=0；
当点C在直线y=-x+b上时，b值最大，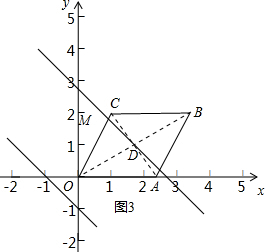
∵点C（1，2），
∴2=-1+b，解得：b=3．
故0≤b≤3．
②连接AC、OB，设AC与OB的交点为D，当直线y=-x+b过点D时，直线y=-x+b将四边形OABC分成面积相等的两部分，如图3所示．
∵OA=OC=$\sqrt{5}$，
∴点A（$\sqrt{5}$，0）．
∵四边形OABC为菱形，C（1，2），A（$\sqrt{5}$，0），
∴点D（$\frac{1+\sqrt{5}}{2}$，1）．
∵直线y=-x+b过点D，
∴1=-$\frac{1+\sqrt{5}}{2}$+b，解得：b=$\frac{3+\sqrt{5}}{2}$．
∴当直线y=kx+b将四边形OABC分成面积相等的两部分时，k=-1，b=$\frac{3+\sqrt{5}}{2}$．

点评 本题考查了菱形的性质、平移的性质以及待定系数法求函数解析式，解题的关键是：（1）找出PC+PM≤AM；（2）①根据题意画出图形，以便确定直线y=kx+b的活动区间；②求出点D的坐标．本题属于中档题，难度不大，解决该题型题目时，根据题意画出图形，利用数形结合来解决问题是关键．