
分析 (1)两个连续整数乘积的倒数等于各自倒数的差,据此可得;
(2)将等式右边通分,依据分式的加法运算后可得$\frac{2(a+b)n+a-b}{(2n-1)(2n+1)}$=$\frac{1}{(2n-1)(2n+1)}$,从而得出关于a、b的方程组,解之可得;
(3)依据以上规律,列项相消求解可得.
解答 解:(1)第n个等式为$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)∵$\frac{a}{2n-1}$+$\frac{b}{2n+1}$=$\frac{a(2n+1)+b(2n-1)}{(2n-1)(2n+1)}$=$\frac{2(a+b)n+a-b}{(2n-1)(2n+1)}$=$\frac{1}{(2n-1)(2n+1)}$,
∴$\left\{\begin{array}{l}{a+b=0}\\{a-b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$,
故答案为:$\frac{1}{2}$,-$\frac{1}{2}$;
(3)原式=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{97}$-$\frac{1}{99}$)
=$\frac{1}{2}$×(1-$\frac{1}{99}$)
=$\frac{1}{2}$×$\frac{98}{99}$
=$\frac{49}{99}$.
点评 本题主要考查数字的变换规律,熟练掌握两个等式前后变化的规律是解题的关键


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
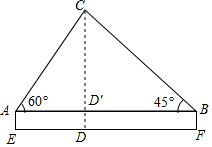 从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米.
从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sinB=$\frac{2}{3}$ | B. | cosB=$\frac{2}{3}$ | C. | tanB=$\frac{2}{3}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
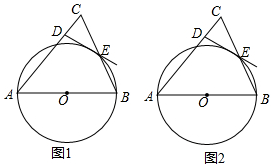 如图1,在△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线ED交AC于点D.
如图1,在△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线ED交AC于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com