
分析 (1)从左到右依次计算即可;
(2)根据分式的除法法则进行计算即可;
(3)、(4)先通分,再把分子相加减即可;
(5)先算括号里面的,再算乘法即可;
(6)先算括号里面的,再算除法即可.
解答 解:(1)原式=$\frac{5x}{9y}$•$\frac{21{x}^{2}}{10y}$
=$\frac{7{x}^{2}}{6{y}^{2}}$;
(2)原式=$\frac{(2x-y)^{2}}{2x-y}$•$\frac{1}{(2x-y)(2x+y)}$
=(2x-y)•$\frac{1}{(2x-y)(2x+y)}$
=$\frac{1}{2x+y}$;
(3)原式=$\frac{{a}^{2}}{a-b}$-$\frac{{b}^{2}}{a-b}$
=$\frac{{a}^{2}-{b}^{2}}{a-b}$
=a+b;
(4)原式=$\frac{{x}^{2}}{x-y}$-$\frac{(x-y)^{2}}{x-y}$
=$\frac{{x}^{2}-{x}^{2}+2xy-{y}^{2}}{x-y}$
=$\frac{2xy-{y}^{2}}{x-y}$;
(5)原式=$\frac{1-a-1}{1-a}$•$\frac{1-{a}^{2}}{{a}^{2}}$
=$\frac{-a}{1-a}$•$\frac{(1-a)(1+a)}{{a}^{2}}$
=-$\frac{1+a}{a}$;
(6)原式=$\frac{(x+2)(x-2)+4}{(x-2)^{2}}$•$\frac{x-2}{x}$
=$\frac{{x}^{2}}{{(x-2)}^{2}}$•$\frac{x-2}{x}$
=$\frac{x}{x-2}$.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
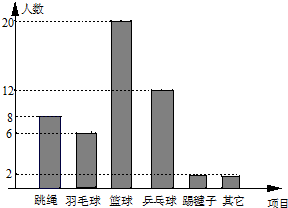 小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )
小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )| A. | 144° | B. | 75° | C. | 180° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
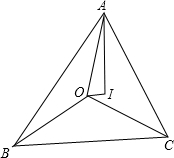 在△ABC中,AB>AC,O、I分别是△ABC的外心和内心,且满足AB-AC=2OI,求证:
在△ABC中,AB>AC,O、I分别是△ABC的外心和内心,且满足AB-AC=2OI,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com